Chapter 3: Feed Forward Neural Net

3.1 Perceptron – 신경망

퍼셉트론이란 뉴런을 모방한 회로를 말한다. 

다만, 이 퍼셉트론은 선형분류라는 특성상 한계가 존재한다.

 §  동그라미와 세모를 분리하려면 어떻게 해야 할까?

 §  y = ax + b 형태의 직선을 이용할 수 있다.

 §  일반화해서 표현해 보자.

 §  Generalization

3.1 Perceptron – AND 분류

3.1 Perceptron – OR 분류

3.1 Perceptron – XOR 분류

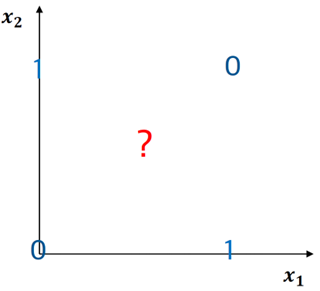
 §  Perceptron은 XOR을 분류하지 못한다…

 §  직선 두 개를 이용하여 XOR 분류를 해결 할 수 있다.

 §  그러면, 어떤 모델을 이용하여 직선 두 개를 나타낼 수 있을까?

3.2.1 Multi-later Perceptron

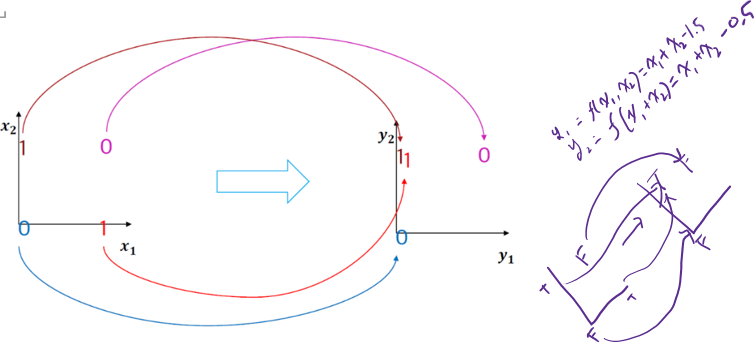
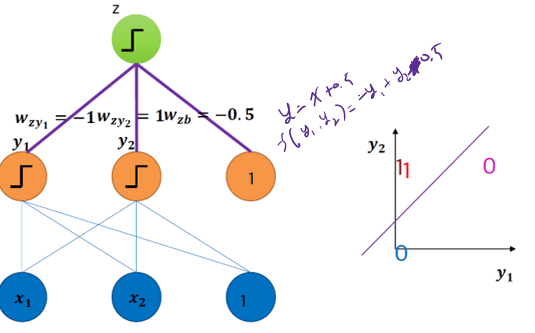
 §  여기서 나온 해결책이 MLP로  layer를 추가하면 해결 가능하다.

 레이어를 추가하면 아래와 같이 공간이 사상되어 선형 분류가 가능해진다. 다만 이는 svm과의 커널 트릭과는 다름에 유의.

3.2.2 Multi layer Perceptron 학습

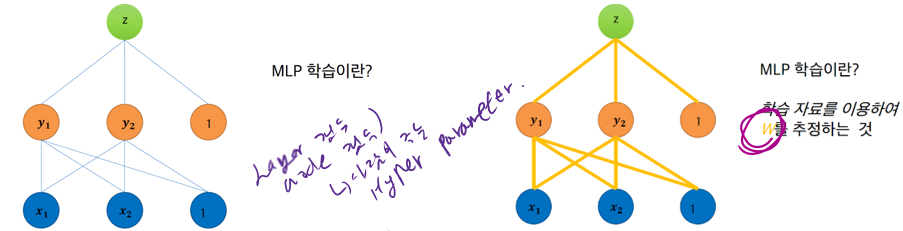
 §  MLP 학습이란?

  • 학습 자료를 이용하여 $W$  를 추정하는 것이다.

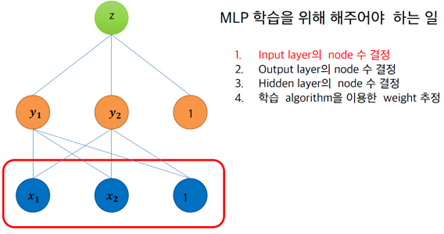
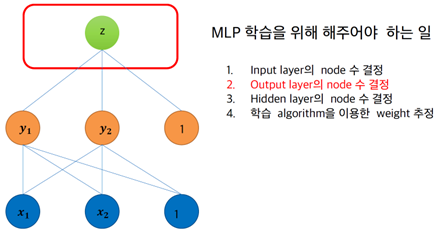
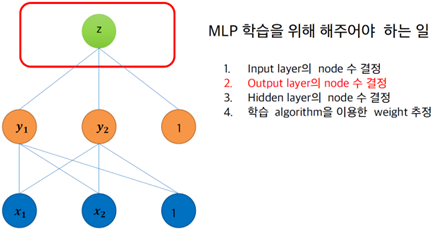
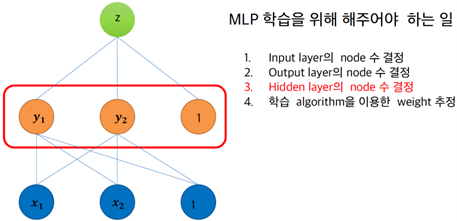
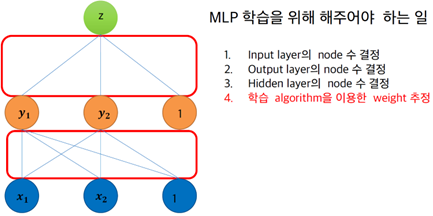
 §  MLP 학습을 위해 해주어야 하는 일

  • Input layer의 node 수 결정

    - Domain에 따라 결정

  • Output layer의 node 수 결정

    - Domain에 따라 결정한다

  • Hidden layer의 node 수 결정

    - 실험을 통해 결정

  • 학습 algorithm을 이용한 weight 추정

    - Back-propagation알고리즘을 이용하여 레이블 된 학습 자료에 최적 weight를 추정한다

3.2.2 Back propagation algorithm

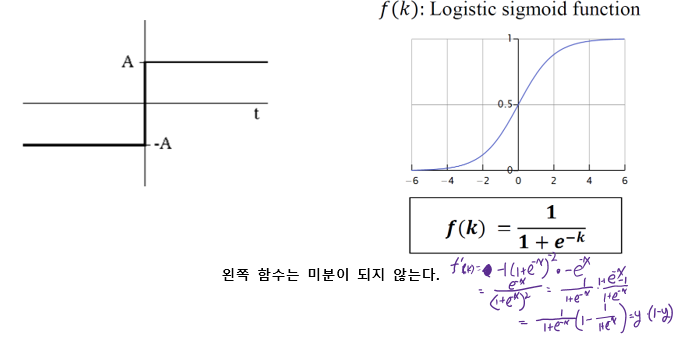
 §  학습은 back propagation 알고리즘으로 수행됨

 §  Activation 함수로는 sigmoid를 이용한다.

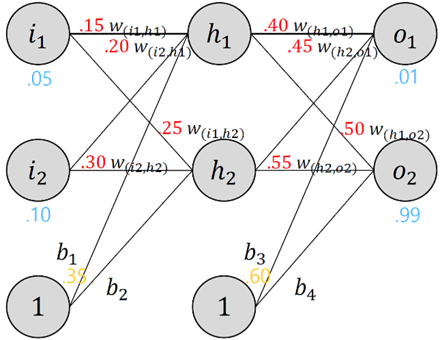
 §  두개의 input, 두개의 hidden neurons, 두개의 output neurons으로 구성된 기본 neural network 구조

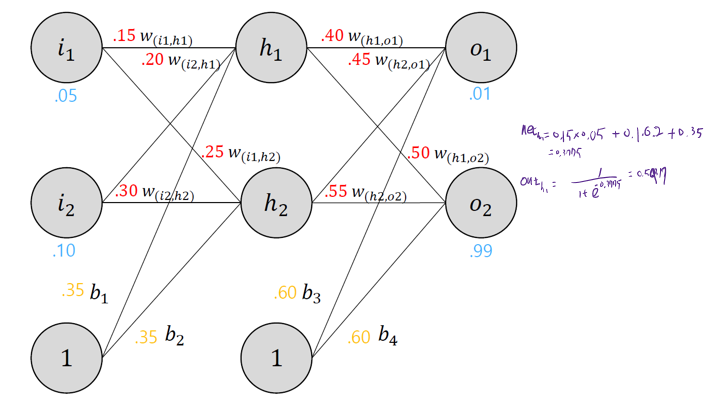
 §  예제

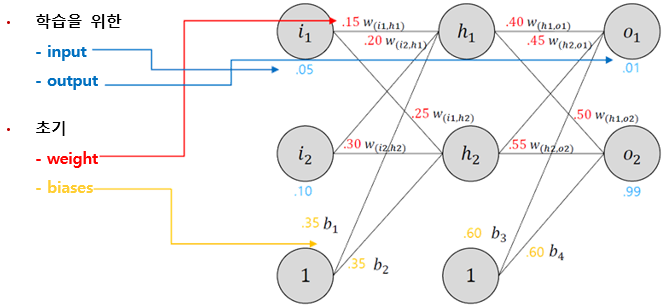
 §  Backpropagation

  • weight들을 최적화하여, 임의의 input/output에 대하여 올바른 답을 낼 수 있도록 함

 §  The forward Pass

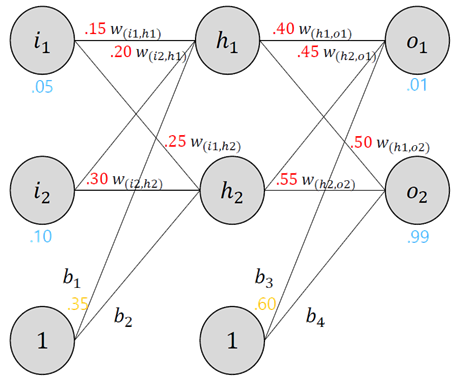
  • $h_{1}$뉴런 input

    - $\text { net }_{h 1}=w_{(i 1, h 1)} * i_1+w_{(i 2, h 1)} * i_2+b_1 * 1$

    - $\text { net }_{h 1}=0.15 * 0.05+0.3 * 0.1+0.35 * 1=0.38075$

  • logistic function을 거친  $h_{1}$ output

    -$\text { out }_{h 1}=\frac{1}{1+e^{- \text {net }_{h 11}}}=\frac{1}{1+e^{-0.3775}}=0.593269992$

  • $h_{2}$에 대하여 같은 과정을 반복

    -$\text { out }_{h 2}=0.596884378$

  • $h_{1}$과 $h_{2}$ 의 방법으로 $o_1$을 진행

    -$\text { net }_{o 1}=w_{(h 1,01)} * \text { out }_{h 1}+w_{(h 2,01)} * \text { out }_{h 2}+b 3 * 1$

    -$\text { net}_{o 1}=0.4 * 0.593269992+0.45 * 0.596884378+0.6 * 1=1.105905967$

    -$\text { out}_{01}=\frac{1}{1+e^{-n e t_{01}}}=\frac{1}{1+e^{-1.105905967}}=0.75136507$

  • $o_{1}$의 방법으로 $o_{2}$를 반복

    -$\text { out }_{o 2}=0.772928465$

 §  Calculating the Total Error

  • 앞서 계산된 뉴런의 output을 squared error function의 input으로 에러를 계산

    - 수식의 계수 ½ 은 미분의 편의성을 위함. 후 약분 됨.

  • 예시

    - $o_1$의 target output = 0.01

    - $o_1$의 neural net output = 0.75136507

    - 따라서, error는 $\begin{aligned} E_{o 1} & =\frac{1}{2}\left(\text { target }_{\text {o1 }}-\text { out }_{\text {o1 }}\right)^2 =\frac{1}{2}(0.01-0.75136507)^2 =0.274811083 \end{aligned}$

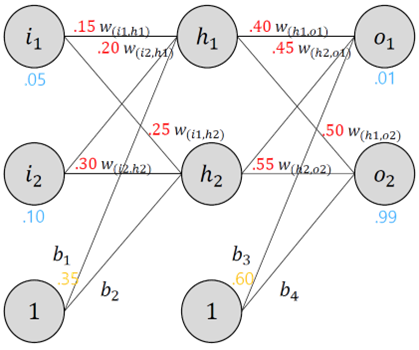
 §  The Backwards Pass

  • Back propagation의 목표인 weight update를 진행

 §  Output Layer

  • The backwards pass

  • 예를 들어, $w_{(h_{1},o_{1})}$를 update 한다면

    - total error에 어느정도 영향을 주는지 알기 위해 편미분을 진행 (체인 룰 적용)

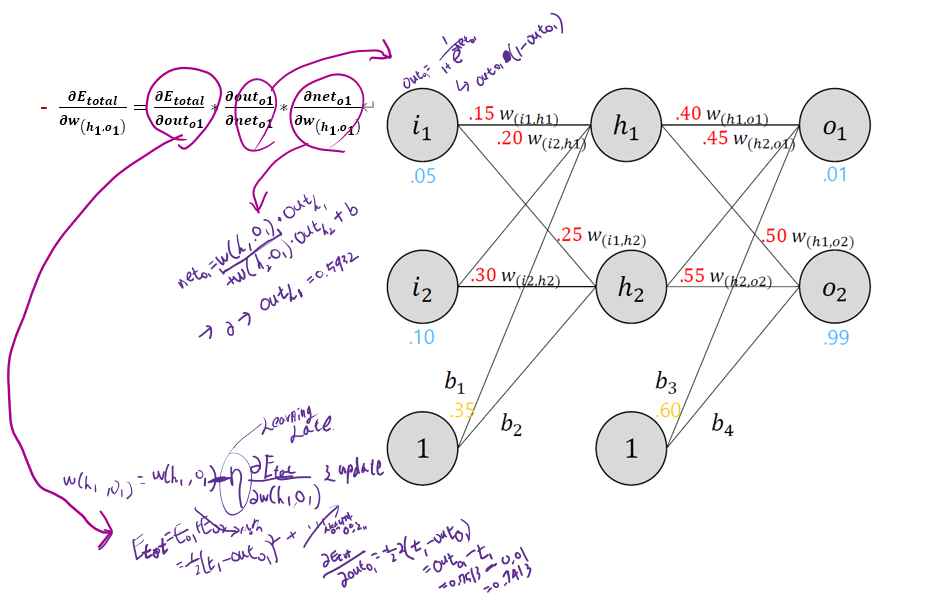
  • 위 내용을 시각화 하면 아래와 같다

  • 각 부분별로 계산을 진행

  • $\frac{\partial E_{\text {total }}}{\partial w_{\left(h_1, \omega_1\right)}} * \frac{\partial \text { out }_{a 1}}{\partial \text { net }_{o 1}} * \frac{\partial E_{\text {total }}}{\partial o u t_{o 1}}=\frac{\partial E_{\text {total }}}{\partial w_{\left(h_1, \omega_1\right)}}$

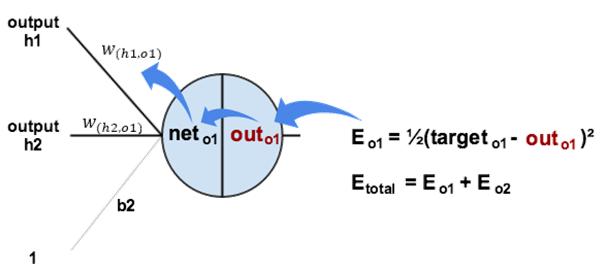
  •  먼저, output($o_1$)의 변화에 대한 total error의 변화를 계산

    -$E_{\text {total }}=\frac{1}{2}\left(\text { target }_{01}-\text { out }_{01}\right)^2+\frac{1}{2}\left(\text { target }_{02}-o u t_{02}\right)^2$

    -$\frac{\partial E_{\text {total }}}{\partial \text { out }}=2 * \frac{1}{2}\left(\text { target }_{o 1}-\text { out }_{01}\right)^{2-1} *-1+0$

    -$\frac{\partial E_{\text {totai }}}{\text { out }_{01}}=-\left(\text { target }_{01}-\text { out }_{01}\right)=-(0.01-0.75136507)=0.74136507$

  • total net input의 변화에 대한 output($o_1$)의 변화를 계산

    - logistic function의 편미분 결과는 $out(1-out)$임

    - $\text { out }{ }_{o 1}=\frac{1}{1+e^{-n e t}}$

    -$\frac{\partial o u t_{o 1}}{\partial e_{o 1}}=\text { out }_{o 1}\left(1-\text { out }_{o 1}\right)=0.75136507(1-0.75136507)=0.186815602$

  • 그리고, $w_{()}$의 변화에 대한 의 변화를 계산

    -$\text { net }_{o 1}=w_{(h 1, o 1)} * \text { out }_{h 1}+w_{(h 2, o 1)} * \text { out }_{h 2}+b_2 * 1$

    - $\frac{\partial n e t_{o 1}}{\partial w_{(\hbar 1,01)}}=1 * \text { out }_{h 1} * w_{\left(h_1, o_1\right)}^{(1-1)}+0+0=\text { out }_{h 1}=0.593269992$

  • 위 결과 식들을 종합

    - $w_{(h_1,o_1)}$ 의 변화에 대한 total error

     *$\frac{\partial E_{\text {total }}}{\partial w_{\left(h_1, o_1\right)}}=\frac{\partial E_{\text {total }}}{\partial o u t_{o 1}} * \frac{\partial o u t_{o 1}}{\partial \text { net }_{o 1}} * \frac{\partial \text { net }_{o 1}}{\partial w_{(h 1, o 1)}}$

     *$\frac{\partial E_{\text {total }}}{\partial w_{(\hbar 1,01)}}=0.74136507 * 0.186815602 * 0.593269992=0.082167041$

  •  error를 감소시키기 위해, 위 식에서 얻은 값을 현재 weight에서 빼준다. 이때 learning rate(eta)을 곱한 뒤 뺀다.

    -$w_{\left(h_1, 0_1\right)}^{+}=w_{\left(h_1, 0_1\right)}-\eta * \frac{\partial E_{\text {total }}}{\partial w_{\left(h_1, 0_1\right)}}=0.4-0.5 * 0.082167041=0.35891648$

  •  동일한 프로세스를 $w^{+}_{(h_1, o_1)}~w^{+}_{(h_2,o_2)}$에 대하여 반복

    -$w_{\left(h_2, o_1\right)}^{+}=0.408666186$
    -$w_{\left(h_1, o_2\right)}^{+}=0.511301270$
    -$w_{\left(h_2, 0_2\right)}^{+}=0.561370121$

  •  weight값 실제 update는 hidden layer에 대해서 새로운 weight을 모두 구한 후 update를 진행

 §  Hidden Layer

  • The backwards pass (Cont.)

    - $w_{(i_1, h_1)}~w_{(i_2, h_2)}$에 대해서 값을 계산

  • output layer에서 진행했던 방식과 유사한 방식

    - 차이점 : 여러 개의 output neurons의 변화량 사용
      ⁎ $h_1$의 out부분이 $o_1, o_2$에 영향을 줌

         $\frac{\partial E_{\text {total }}}{w_{(i 1, \boldsymbol{h} \mathbf{1})}}=\frac{\partial E_{\text {total }}}{\partial o u t_{h \mathbf{1}}} * \frac{\partial o u t_{\boldsymbol{h} \mathbf{1}}}{\partial n e t_{\boldsymbol{h} 1}} * \frac{\partial \text { net }_{\boldsymbol{h} \mathbf{1}}}{\partial w_{(i 1, \boldsymbol{h} \mathbf{)}}}$

                    **$\frac{\partial E_{\text {total }}}{\partial o u t_{h 1}}=\frac{\partial E_{o 1}}{\partial o u t_{h 1}}+\frac{\partial E_{o 2}}{\partial o u t_{h 1}}$

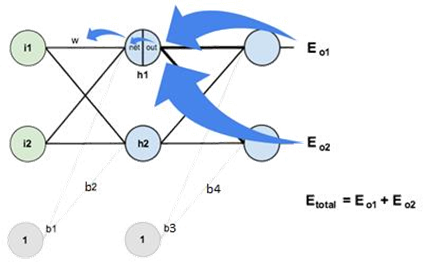
 §  Hidden Layer (Cont.)

  • $\frac{\partial E_{o 1}}{\partial o u t_{h 1}}$계산시 앞서 계산한 $\frac{\partial E_{o 1}}{\partial n e t_{h 1}}$을 사용

    -$\frac{\partial E_{o 1}}{\partial o u t_{h 1}}=\frac{\partial E_{o 1}}{\partial \text { net }_{o 1}} * \frac{\text { net }_{o 1}}{\partial o u t_{h 1}}$
    -$\frac{\partial E_{01}}{\partial n e t_{o 1}}=\frac{\partial E_{01}}{\partial o u t_{o 1}} * \frac{\partial o u t_{o 1}}{\partial n e t_{01}}=0.74136507 * 0.186815602=0.138498562$

  •  $\frac{\partial n e t_{o 1}}{\partial o u t_{h 1}}$와 $w_{(h_1, o_1)}$이 같으므로

    -$\text { net }_{o 1}=w_{(h 1, o 1)} * \text { out }_{h 1}+w_{(h 2,01)} * \text { out }_{h 2}+b 3 * 1$
    -$\frac{\partial n e t_{o 1}}{\partial o u t_{h 1}}=w_{(h 1, o 1)}=0.40$

  • 위 식들을 합쳐주면

    -$\frac{\partial E_{o 1}}{\partial \text { out }_{h 1}}=\frac{\partial E_{o 1}}{\partial \text { net }_{o 1}} * \frac{\partial n e t_{o 1}}{\partial \text { out }_{h 1}}=0.138498562 * 0.40=0.055399425$

  • 같은 방식으로 $\frac{\partial E_{o 2}}{\partial o u t_{h 1}}$를 계산

    ⁻ $$\frac{\partial E_{o 2}}{\partial \text { out }}=-0.019049119$$

  • 따라서 $\frac{\partial E_{\text {total }}}{\partial o u t_{h 1}}$계산 가능

    ⁻$\frac{\partial E_{\text {total }}}{\partial \text { out }_{h 1}}=\frac{\partial E_{o 1}}{\partial o u t_{h 1}}+\frac{\partial E_{o 2}}{\partial o u t_{h 1}}=0.055399425+-0.019049119=0.036350306$

  • $\frac{\partial E_{\text {total }}}{\partial o u t_{h 1}}$를 얻었으므로, 각 weight에 대해 $\frac{\text { oout }_{h 1}}{\partial \text { net }_{h 1}}$와 $\frac{\partial n e t_{h 1}}{\partial w}$를 계산

    -$\text { out }_{\boldsymbol{h} \mathbf{1}}=\frac{1}{1+e^{- \text {net }_{h 1}}}$$
    -$\frac{\text { ouut }_{h 1}}{\partial \text { net }_{h 1}}=\text { out }_{h 1}\left(1-\text { out }_{h 1}\right)=0.59326999(1-0.59326999)=0.241300709$

  • output 뉴런에서 했던 방식을 적용하여, $w_{(i_1, h_1)}$에 대한 total net input to $h_1$ 의 편미분을 계산

    -$\text { net }_{h 1}=w_{(i 1, h 1)} * i_1+w_{(i 2, h 1)} * i_2+b 1 * 1$
    -$\frac{\partial n e t_{h 1}}{\partial w_{(i 1, h 1)}}=i_1=0.05$

  • 위 식을 모두 합치면$\frac{\partial E_{\text {total }}}{\partial w_{(i 1, h 1)}}=\frac{\partial E_{\text {total }}}{\partial o u t_{h 1}} * \frac{\partial o u t_{h 1}}{\partial n e t_{h 1}} * \frac{\partial n e t_{h 1}}{\partial w_{(i 1, h 1)}}$

    -$\frac{\partial E_{\text {total }}}{\partial w_{\left(i_1, h_1\right)}}=0.036350306 * 0.241300709 * 0.05=0.000438568$

  • $w_{(i_1, h_1)}$을 update

    -$w_{\left(i_1, h_1\right)}^{+}=w_{\left(w_1, h_1\right)}-\eta \frac{\partial E_{\text {total }}}{\partial w_{\left(i_1, h_1\right)}}=0.15-0.5 * 0.000438568=0.149780716$

  • 같은 방법으로 $w_{\left(i_2, h_1\right)}^{+} \sim w_{\left(i_2, h_2\right)}^{+}$ 를 반복

    -$w_{\left(i_2, h_1\right)}^{+}=0.19956143$

    -$w_{\left(i_1, h_2\right)}^{+}=0.24975114$
    -$w_{\left(i_2, h_2\right)}^{+}=0.29950229$

 §  학습 결과 예제

  •  1st error = 0.298371109

  •  2nd error = 0.291027924

    - …
    - …

  •  10000th error = 0.00035085

    - 이때, 두 output 뉴런을 보면,

     * 0.015912196 (vs 0.01 target)
     * 0.984065734 (vs 0.99 target)

흔히 게임이론이라고 하면, 게임을 만드는 방법으로 생각하고는 한다.

나에게 누군가 게임이론이 무엇이냐고 질문한다면, "특정 관념에 기초한 최적화 기법" 이라는 말을 할 것이다. 

게임이론이란, 의사결정, 분배에 대한 문제로써 모든 상황과 문제를 게임 상황에 대입시켜 계산하기 위한 기법이다. 

게임이론은 몇가지 테마로 나뉘게 되는데, 대표적으로 협력게임과 비협력 게임이다. 다만, 이를 단순히 구분하기는 어려운 것이 협력게임에서도 (예를들면 경쟁이 아예 없다면 사회의 발전이 어려울 것이다.) 계산과정에서 비협력게임을 도입하는 경우도 존재한다.

이 글에서 설명할 바게닝은 전통적으로 협력게임에 속한다.

바게닝을 접하면 가장 많이 접하게 되는 내쉬 바게닝 솔루션은, Feasible space에서 내쉬곱의 최대가 되는 지점을 찾는 방법으로, 수식으로 표현하자면 다음과 같다.

Find NBS for Two-person bargaining problem

$$\begin{aligned} & S=\left\{\left(y_1, y_2\right) \mid 0 \leq y_1 \leq 30,0 \leq y_2 \leq 30-y_1\right\} \\ & d=(0,0) \end{aligned}$$
$$\begin{aligned} & \operatorname{NBS}(S)=\operatorname{argmax}\left(y_1 y_2\right) \\ & y_1 y_2=y 1\left(30-y_1\right) \\ & y_1\left(30-y_1\right) \frac{d}{d y_1}=0 \Leftrightarrow 2 y_1=30 \\ & y_1=15, y_2=15 \end{aligned}$$

$$S=\left\{\left(y_1, y_2\right) \mid 0 \leq y_1 \leq 30,0 \leq y_2 \leq \sqrt{30-y_1}\right\}$$
$$\begin{aligned} & y_1 y_2=y_1 \sqrt{30-y_1} \\ & y_1 \sqrt{30-y_1} \frac{d}{d y_1}=0 \\ & \sqrt{30-y_1}+\frac{-1 \cdot y_1}{2 \sqrt{30-y_1}}=\frac{60-3 y_1}{2 \sqrt{30-y_1}}=0 \\ & y_1=20, y 2=\sqrt{10} \end{aligned}$$

$$\begin{aligned} & N B S=\operatorname{argmax}\left(U_E U_C \mid U_E, U_C \in \operatorname{scenario}(n)\right) \\ & E S=\left(U_E, U_C \mid U_E=U_C,\left(U_E, U_C \in \operatorname{scenario}(n)\right)\right) \\ & K S B S=\left(U_E, U_C \mid U_E, U_c \in \operatorname{scenario}(n) \text { and } U_E, U_C \in d+(a-d)\right) \\ & N=\{E, C\} . T=[0,1] \end{aligned}$$

$$\begin{aligned} & \text { scenario1. } U_E(t)=1-t, U_C(t)=t \\ & N B S:\left(U_E U_C\right)^r=1-2 t=0, t=0.5,\left(U_E, U_C\right)=(0.5,0.5) \\ & E S: U_E=U_C \Leftrightarrow 1-t=t \Leftrightarrow t=0.5,\left(U_E, U_C\right)=(0.5,0.5) \\ & K S B S: \max \left(U_E, U_C\right)-\min \left(U_E, U_C\right)=(1,1) \Leftrightarrow U_E=U_C \\ & 1-t=t \Leftrightarrow t=0.5,\left(U_E, U_C\right)=(0.5,0.5) \end{aligned}$$

$$\begin{aligned} & \operatorname{scenario2.} U_E(t)=1-t, U_C(t)=t^{\frac{1}{2}} \\ & N B S:\left(U_E U_C\right)^{\prime}=1 / 2 \sqrt{t}-3 / 2 \cdot \sqrt{t}=(1-3 t) / 2 \sqrt{t}=0, t=1 / 3,\left(U_E, U_C\right)=(2 / 3, \sqrt{1 / 3}) \\ & E S: U_E=U_C \Leftrightarrow 1-t=\sqrt{t} \Leftrightarrow t=3 / 2-\sqrt{5} / 2 \\ & \left(U_E, U_C\right)=((\sqrt{5}-1) / 2,(\sqrt{6-2 \sqrt{5}}) / 2)=\left((\sqrt{5}-1) / 2,\left(\sqrt{(1-\sqrt{5})^2}\right) / 2\right)=((\sqrt{5}-1) / 2,(\sqrt{5}-1) / 2) \\ & K S B S: \max \left(U_E, U_C\right)-\min \left(U_E, U_C\right)=(1,1) \Leftrightarrow U_E=U_C, \text { same as ES } \end{aligned}$$

$$\begin{aligned} & \text { scenario3. } U_E(t)=(1-t)^{\frac{1}{2}}, U_C(t)=t^{\frac{1}{2}} \\ & N B S:\left(U_E U_C\right)^{\prime}=\frac{1-2 t}{2 \sqrt{t-t^2}}=0, t=0.5,\left(U_E, U_C\right)=(\sqrt{1 / 2}, \sqrt{1 / 2}) \\ & E S: U_E=U_C \Leftrightarrow \sqrt{1-t}=\sqrt{t} \Leftrightarrow t=0.5,\left(U_E, U_C\right)=(\sqrt{1 / 2}, \sqrt{1 / 2}) \\ & K S B S: \max \left(U_E, U_C\right)-\min \left(U_E, U_C\right)=(1,1) \Leftrightarrow U_E=U_C, \text { same as } E S \end{aligned}$$

$$\begin{aligned} & \text { scenario4. } U_E(t)=2(1-t), U_C(t)=t \\ & N B S:\left(U_E U_C\right)^{\prime}=2-4 t=0, t=0.5 \\ & E S: U_E=U_C \Leftrightarrow 2-2 t=t \Leftrightarrow t=2 / 3 \\ & K S B S: \max \left(U_E, U_C\right)-\min \left(U_E, U_C\right)=\operatorname{vector}(2,1) \Leftrightarrow U_E=2 U_C \\ & 2-2 t=2 t \Leftrightarrow t=0.5 \end{aligned}$$

이전부터 미뤄오던  앞마당 화단쪽 우수관 보수 공사를 하기로 했다.

기존의 상황은 약 50년도 더 전에, 화강석을 쌓아서 우수로가 확보되어 있으며, 거기에 시 관로가 연결되어 있던 상황.

이전에 살던 세입자들이 아무렇게나 쓰다보니 이것저것 많이 쌓여있다.

원래 이 부분에 플륨관만 묻으려고 했으나...

물이 나가는 쪽이 잘 안나가는 상황이었다.

차가 지나다니는 곳 아래에는 화강석을 쌓아 만든 수로가 있고, 그 위헤 큰 판석이 덮혀있고, 콘크리트 포장이 되어있는 상황.

이것으로 아버지와 많이 마찰이 있었다. 나는 청소업체를 불러 내부 상황을 파악하고 필요한 곳만 보수를 하자.

화강암이 요즘 자재보다 오히려 남은 수명이 길 것이다.

아버지는 아니다. 이거 한게 언젠데, 결국 뜯어내야 한다.

죽은사람 소원도 들어준다는데, 산사람 소원 못 들어주겠는가.. 결국 다 뜯었다.

사진을 못 찍었고 밖에서는 안보이지만 내부를 확인하다보니, 곡선으로 돌을 쌓아 만든 수로가 정말 아름다웠다.

옜날에 어떻게 이런것을 만들었나, 그리고 지금도 이런것을 해주는 곳이 있을까 싶었다.

아버지도 야...튼튼하게 하긴했다....라고 하셔서 더 열이 받았다. 뜯지 말자니깐....

뜯고보니...결국 내 말이 맞았다.. 시 관로와 이어지는 콘크리트 관만 삭아 부셔져 있었고, 뜯으면서도 아 이거 백년은 더 가겠는데 싶었던 애꿏은 수로만 부셔버렸던것....

부랴부랴 자재를 사다가 연결한다.

300mm1종 이중벽관과 250mm 1종 이중벽관, 맨홀을 사왔다.

시관로와 맨홀을 연결하고, 우수로와 기존의 모이는 관거들을 다시 연결한다.

자재를 사다놨더니 고양이들이 캣타워인줄 안다.

우수관을 연결하고, 맨홀에는 공구리를 친다.

그리고 플륨관을 다시 놓는다.

그리고 다시 포장

보양

갑작스래 일이 너무 커졌지만... 겨우겨우 공사를 마무리했다.

추가로 밭의 배수로도 정비를 했다.

정말.. 토목관련은 별로 하고 싶지가 않지만, 보통 문제가 생겨 보수하는 곳은 물의 문제인 것 같다.

남은것은 슬레이트를 걷어낸 축사 지붕 씌우기와, 건조장 지붕 교체, 본채 파고라 보수이다.