</p
4.1 Introduction
- 아래와 같은 공이 있을 때 다음 위치를 예측 할 수 있을까?

- 이전 시점들의 정보가 주어진다면?

4.1.1 Examples of Sequence Data


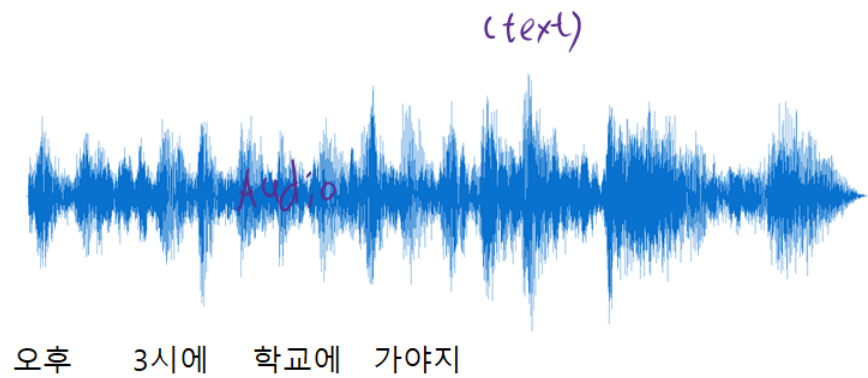
4.1.2 Sequence Modeling Applications

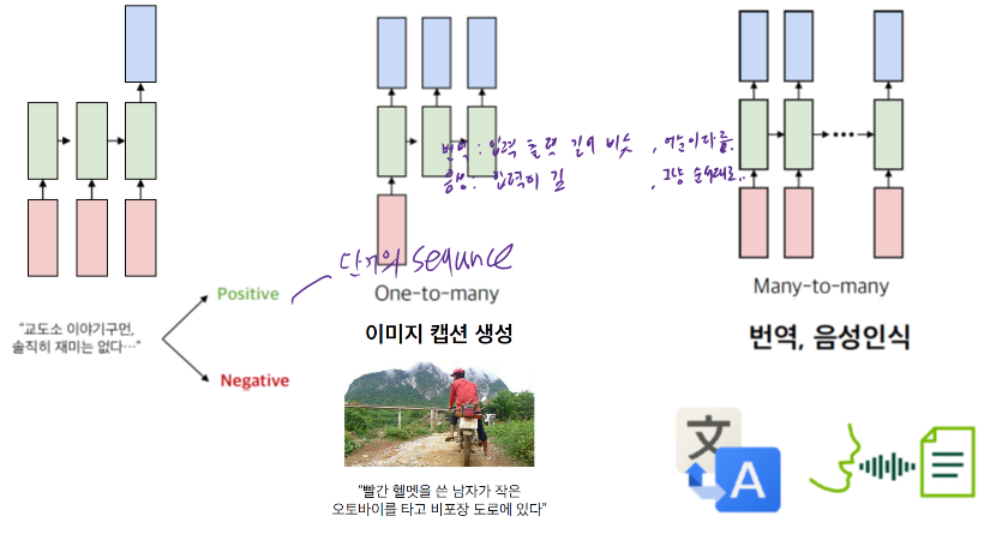
4.1.2 Handling Individual Time steps
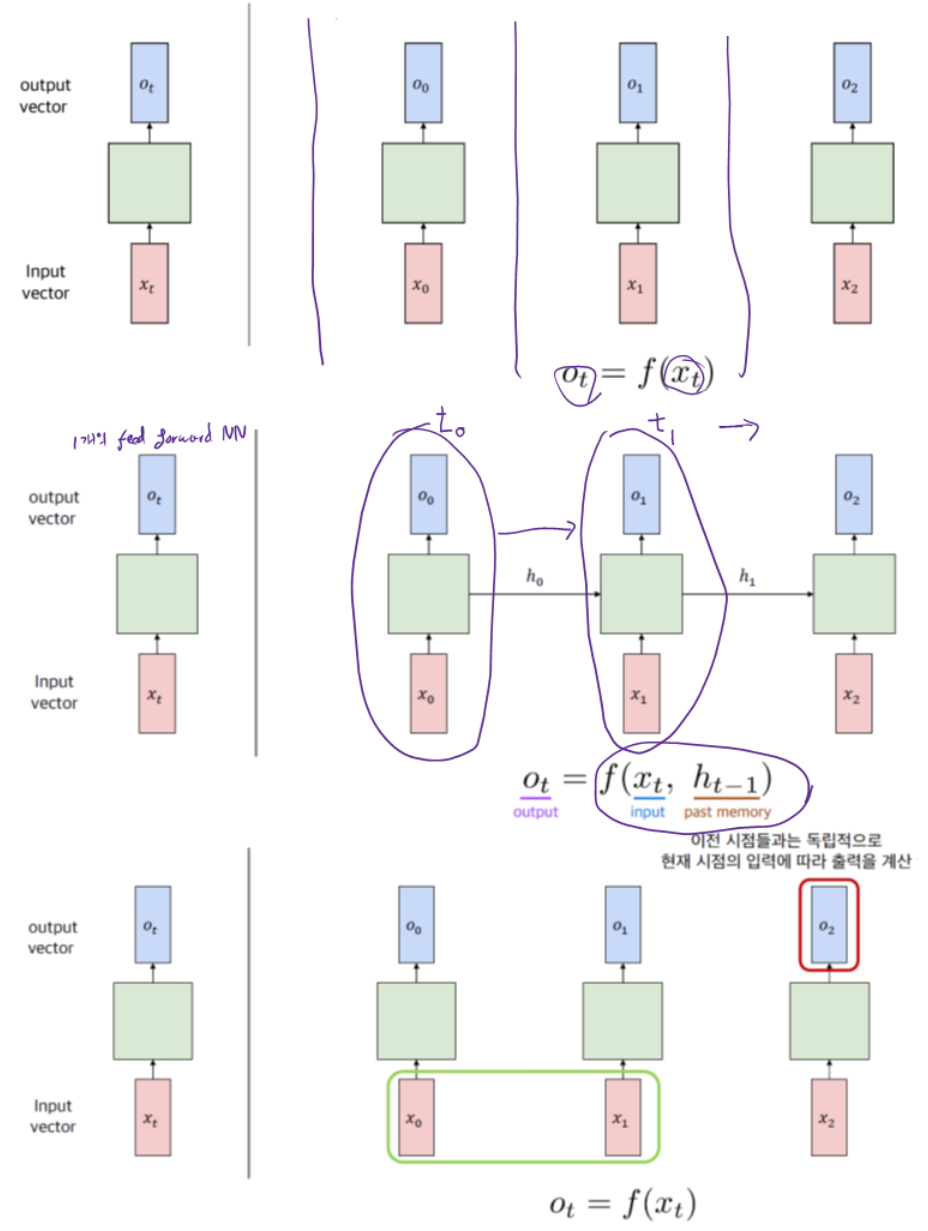
4.2 Neurons with Recurrence
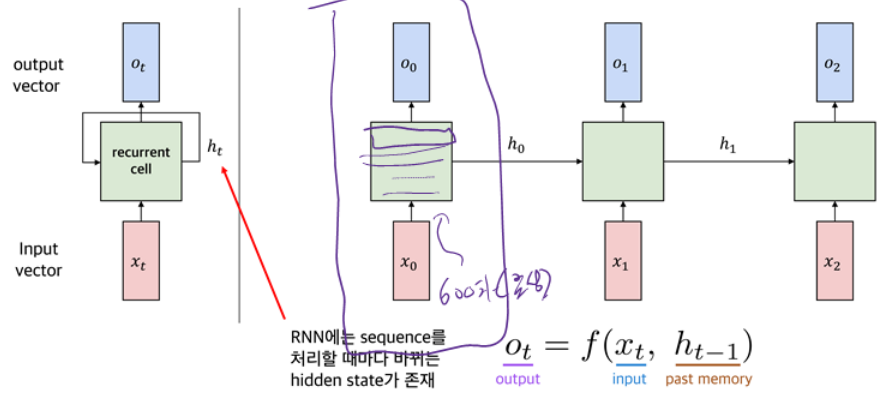
4.2.1 Recurrent Neural Networks (RNNs)

4.2.2 Activation Functions

4.2.3 The Role of the Hidden Layer
The role of the hidden layer is to map samples from the input space to the hidden layer space.
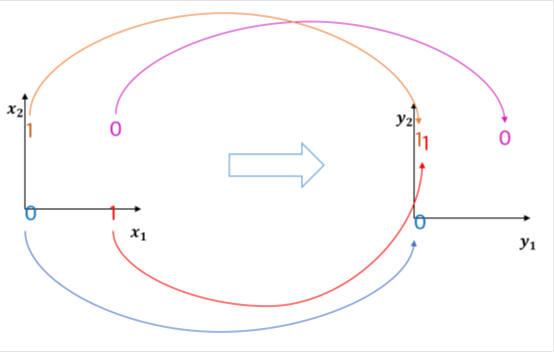
4.2.4 RNN State Update and Output

4.2.5 RNN : Graph Representation

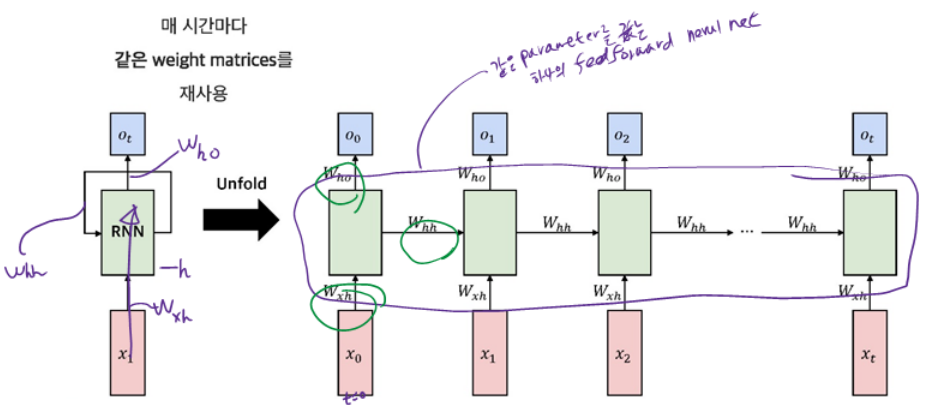
4.2.6 RNNs : Computational Graph Across Time

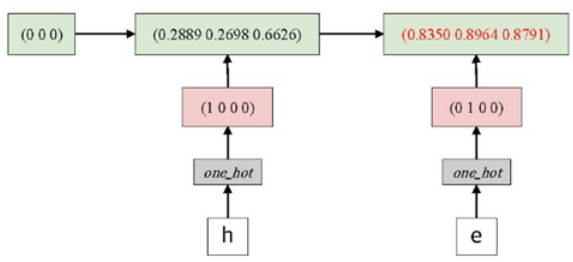
4.2.7 Example : Predict Sequence of Character
§ 다음 문자를 예측하는 네트워크를 설계
● "hello"라는 단어 기준
● h,e, 1,1 이 입력으로 들어왔을 때 o 를 예측
- {'h': 0, 'e':1, 'l':2, 'o':3\}
● one-hot encoding
| h | [1,0,0,0] |
| e | [0,1,0,0] |
| l | [0,0,1,0] |
| o | [0,0,0,1] |
● hidden layer는 1 층의 RNN을 사용
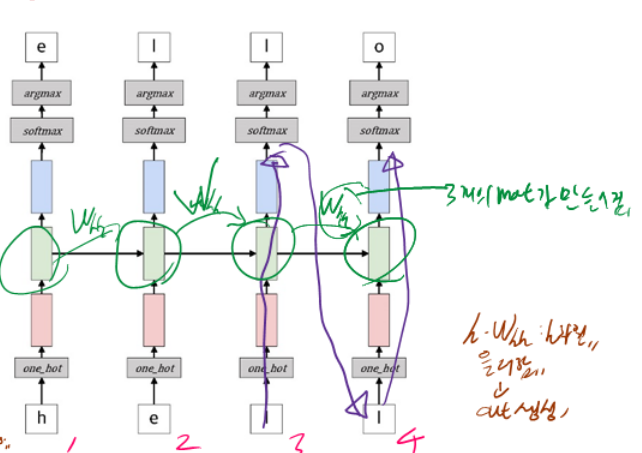
전체적으로 봤을 땐 Language 모델, $t=1$ 일 때 $h$ 오면 e 예측 $t=2$ 일때 e 오면 i를 예측 한다.
● 다음과 같은 one-hot encoding을 입력으로 받음

● RNN model :
$$
\begin{aligned}
& o_{t}=h_{t} W_{h o} \\
& h_{t}=\tanh \left(h_{t-1}\left(W_{h h}+x_{t}\left(W_{x h}\right)\right)\right.
\end{aligned}
$$
● $W_{x h}$ 는 다음과 같은 0 에서 1 사이의 값으로 ($4 \times 3$ )행렬을 random initialize
$$
W_{x h}=\left(\begin{array}{lll}
0.2973 & 0.2766 & 0.7974 \\
0.3869 & 0.9170 & 0.4125 \\
0.5538 & 0.5646 & 0.5026 \\
0.2206 & 0.6801 & 0.3880
\end{array}\right)
$$
● $x_{1} W_{x h}$ 는 다음과 같이 계산
$
x_{1} W_{x h}=\left(\begin{array}{llll}
(1 & 0 & 0 & 0
\end{array}\right) \times\left(\begin{array}{lll}
0.2973 & 0.2766 & 0.7974 \\
0.3869 & 0.9170 & 0.4125 \\
0.5538 & 0.5646 & 0.5026 \\
0.2206 & 0.6801 & 0.3880
\end{array}\right)=\left(\begin{array}{llll}
0.2973 & 0.2766 & 0.7974
\end{array}\right)
$$

● $W_{h h}$ 는 다음과 같은 0 에서 1 사이의 값으로 random initialized $3 \times 3$ 행렬
$$
W_{h h}=\left(\begin{array}{lll}
0.3152 & 0.5083 & 0.9454 \\
0.3008 & 0.6058 & 0.2999 \\
0.9741 & 0.3419 & 0.9133
\end{array}\right)
$$
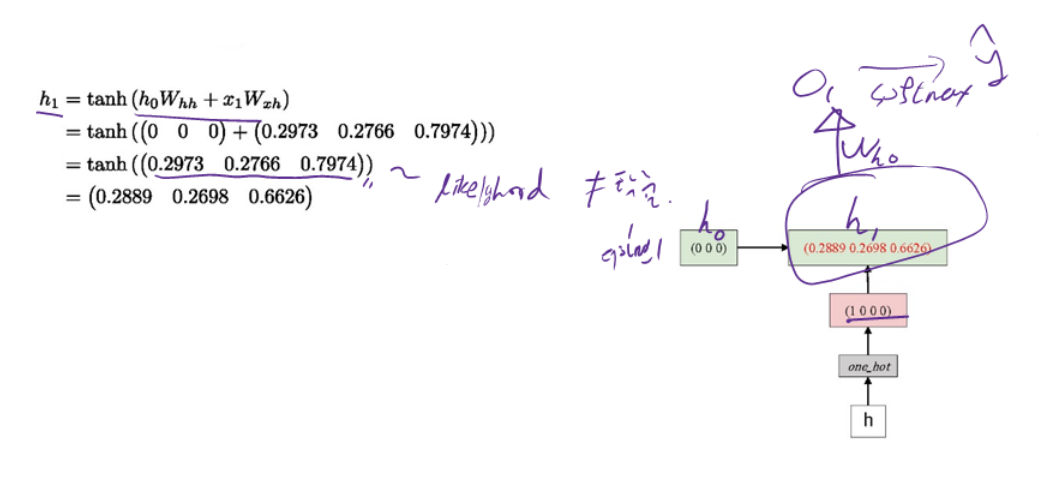
● $h_{t-1} W_{h h}$ 를 계산하기 위해서는 initial hidden state $h_{0}$ 가 필요
- 일반적으로 initial hidden state로는 $O$ 를 사용(영행렬)

● $h_{1}$ 은 다음과 같이 update
● $W_{h y}$ 는 같은 0 에서 1 사이의 값으로 random initialized $3 \times 4$ 행렬
$
W_{h o}=\left(\begin{array}{llll}
0.3189 & 0.6216 & 0.5164 & 0.7501 \\
0.0260 & 0.6230 & 0.0179 & 0.6123 \\
0.1320 & 0.9009 & 0.3873 & 0.8142
\end{array}\right)
$

● $o_{1}$ 의 softmax 값과 이중 가장 큰 값의 index를 추출하는 argmax를 적용

● $W_{x h}, W_{h h}$ 는 동일한 weight를 사용
● $x_{2}W_{x h}$와 $h_{1}W_{h h}$는 다음과 같이 계산한다.
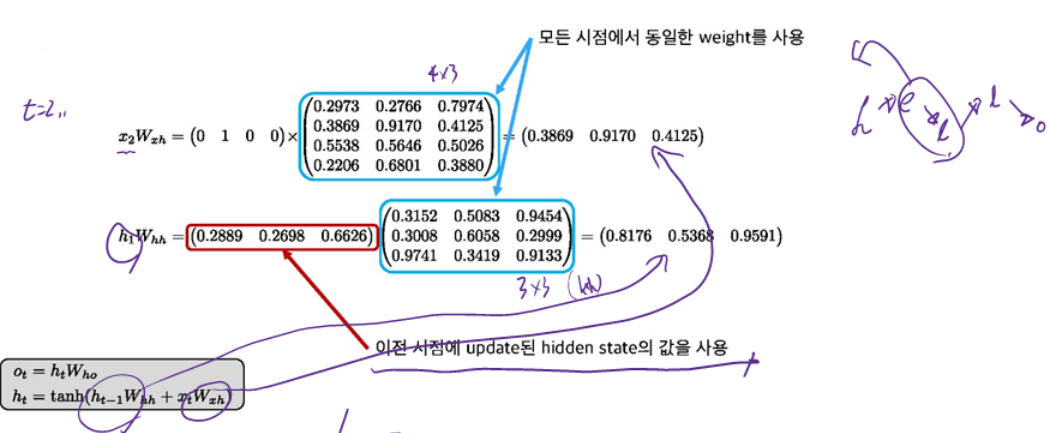
● $h_{2}$ 는 다음과 같이 update
$$
\begin{aligned}
& h_{2}=\tanh \left(h_{1} W_{h h}+x_{2} W_{x h}\right) \\
& =\tanh \left(\left(\begin{array}{lll}
0.8176 & 0.5368 & 0.9591
\end{array}\right)+\left(\begin{array}{lll}
0.3869 & 0.9170 & 0.4125
\end{array}\right)\right) \\
& =\tanh \left(\left(\begin{array}{lll}
1.2045 & 1.4538 & 1.3716
\end{array}\right)\right) \\
& =\left(\begin{array}{lll}
0.8350 & 0.8964 & 0.8791
\end{array}\right)
\end{aligned}
$$
● $o_2$는 시점 1에서와 동일한 방법으로 계산할 수 있다.
$
\begin{aligned}
o_2 & =h_2 W_{h o} \\
& =\left(\begin{array}{lll}
0.8350 & 0.8946 & 0.8791
\end{array}\right)\left(\begin{array}{llll}
0.3189 & 0.6216 & 0.5164 & 0.7501 \\
0.0260 & 0.6230 & 0.0179 & 0.6123 \\
0.1320 & 0.9009 & 0.3873 & 0.8142
\end{array}\right) \\
& =\left(\begin{array}{llll}
0.4056 & 1.8696 & 0.7877 & 1.8910
\end{array}\right)
\end{aligned}
$
이때 $o_2$는 확률이 아님에 유의.
$
\begin{aligned}
& \left.\operatorname{softmax}\left(o_2\right)=\operatorname{softmax}\left(\begin{array}{llll}
0.4056 & 1.8696 & 0.7877 & 1.8910
\end{array}\right)\right) \\
& =\left(\begin{array}{llll}
0.0892 & 0.3858 & 0.1308 & 0.3942
\end{array}\right)
\end{aligned}
$

● 잘못된 예측 발생
- 올바른 예측은 2:1이 되어야 한다.

● 올바르게 학습된 RNN Model

4.3 RNN 학습
4.3.1 RNNs : Computational Graph Across Time
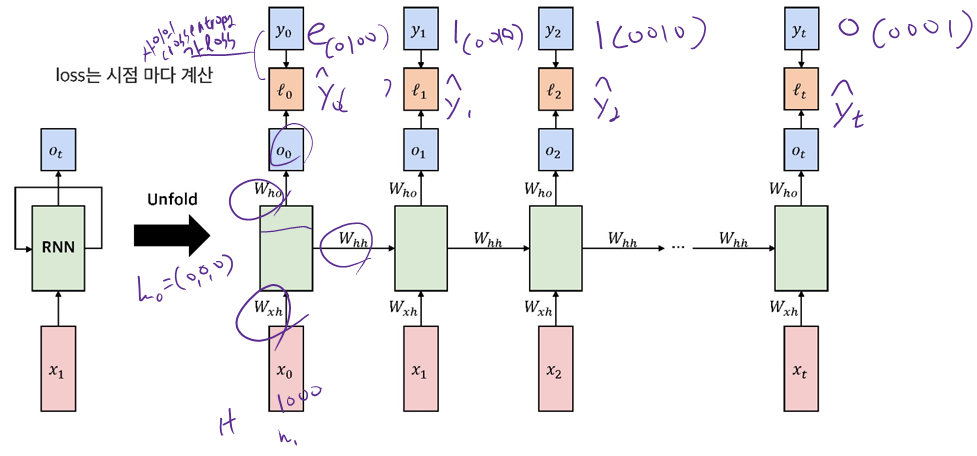

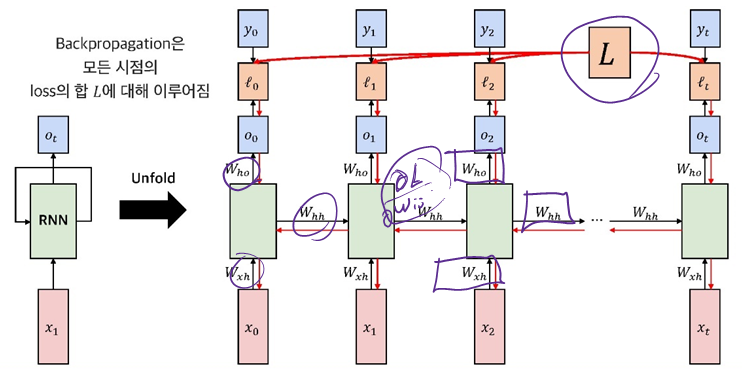
4.3.2 Backpropagation Through Time(BPTT)
Backpropagation through time을 계산 하기 위하여 다음과 같은 RNN 모델을 정의한다.
$h_t = f(X_t \cdot W_{xh} + h_{t-1}\cdot W_{hh})$ ($f$ is activation function)
$o_t = h_t \cdot W_(h0)$
$\hat{y_{t}}=\text{softmax}(o_t)$
이때, $o_{t}$ 는 출력 logit이고 $\hat{y}_{t}$ 는 여기에 SoftMax를 취한 값이다.$C$ 개의 Class를 갖는 출력에 대한 cross entropy를 이용할 때, 시점 t 애서의 정답 $y_{t}$ 에 대한 loss $\ell_{t}$ 를 이용하여 길이 $T$ 의 sequence에 대한 총 loss function 은 다음과 같이 주어진다

Hidden state를 출력과 연결하는 weight와 관련된 gradient를, 즉 $W_{h o}$ 의 속하는 가중치 $w_{i j}$ 에 대하여 계산한다. $w_{i j}$ 는 hidden state의 $i$ 번째 unit을 $j$ 번째 출력 unit에 연결하는 welght이다.

$w_{i j}$ 에 대한 loss function $L$ 에 관한 식을 계산 하기 위해서는 각 시점에서의 gradient를 합산 해야한다. 그러므로 $\frac{\partial L}{\partial w_{i j}}$ 에 대한 식은 다음과 같아진다.
$
\frac{\partial L}{\partial w_{i j}}=\sum_{t=1}^{T} \frac{\partial \ell_{t}}{\partial w_{i j}}=\sum_{t=1}^{T} \frac{\partial \ell_{t}}{\partial \hat{y}_{t}^{(j)}} \frac{\partial \hat{y}_{t}^{(j)}}{\partial o_{t}^{(j)}} h_{t}^{(i)}
$
$\frac{\partial L}{\partial w_{i j}}$ 에 대한 식에서 각 항들의 값들은 다음과 같이 구할 수 있다.
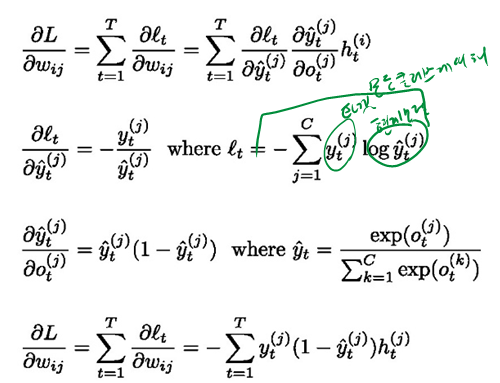
다음으로 $T-1$ 시점에서의 hidden state와 $T$ 시점의 hidden state의 weight, 즉 $W_{h h}$ 에 속하는 weight $u_{k i}$ 에 대해 계산한다. $u_{k i}$ 는 hidden state 내의 $k$ 번째 unit과 $i$ 번째 unit을 연결하는 weight이며, hidden state는 이전 시점의 값에 따라 변경되기 때문에 이를 이해하기 위해 시점 $t$ 에서 $i$ 번째 hidden state unit, 즉 $h_{t}^{(i)}$ 에 대해$
h_{t}^{(i)}=f\left(\sum_{l=1}^{N} u_{l i} h_{t-1}^{(l)}+\sum_{m=1}^{D} v_{m i} x_{t}^{(m)}+b_{h i}\right)
$로 계산된다
weight $u_{k i}$ 에 대한 t 시점에서의 loss function에 대한 gradient는 다음과 같다.
$
\frac{\partial \ell_{t}}{\partial u_{k i}}=\frac{\partial \ell_{t}}{\partial h_{t}^{(i)}} \frac{\partial h_{t}^{(i)}}{\partial u_{k i}}
$
여기서의 $c_{t}^{(i)}$ 는 다음과 같다.
$
c_{t}^{(i)}=\sum_{l=1}^{N} u_{l i} h_{t-1}^{(l)}+\sum_{m=1}^{D} v_{m i} x_{t}^{(m)}
$
$h_{t-1}^{(i)}$ 는 점화식에 의해 $f\left(u_{k i} h_{t-2}^{(k)}+u_{i i} h_{t-2}^{(i)}+c_{t-1}^{(i)}\right)$ 로 표현 가능하므로 계산하려는 weight $u_{k i}$ 와 $h_{t-1}^{(i)}$ 에 관한 항으로 정리하며, 시점 t 에서의 점화식은 첫번째 시점까지 계속 될 것이므로, $\mathrm{t}=\mathrm{t}$ 에서 부터 $\mathrm{t}=1$ 까지의 모든 gradient의 합을 고려해야한다. weight $u_{k i}$ 에 관한 $h_{t}^{(i)}$ 의 gradient가 점화식에 의해 정의 되므로, $\mathrm{u}_{\mathrm{ki}}$ 에 대한 $h_{t}^{(i)}$ 편미분은 다음과 같이 정리할 수 있다.
$
\begin{gathered}
h_{t}^{(i)}=f\left(u_{k i} h_{t-1}^{(k)}+u_{i i} h_{t-1}^{(i)}+c_{t}^{(i)}\right) \\
\frac{\partial h_{t}^{(i)}}{\partial u_{k i}}=\sum_{t^{\prime}=1}^{t} \frac{\partial h_{t}^{(i)}}{\partial h_{t^{\prime}}^{(i)}} \frac{\partial h_{t^{\prime}}^{(i)}}{\partial u_{k i}}
\end{gathered}
$
$\frac{\bar{\partial} h_{t^{\prime}}^{(i)}}{\partial u_{k i}}$ 닌 $_{h_{t^{\prime}-1}^{(i)}}$ 를 상수로 유지한 채 계산한 $u_{k i}$ 에 대한 $h_{t}^{(i)}$ 의 local gradient를 나타낸다.
$
\frac{\partial \ell_{t}}{\partial u_{k i}}=\sum_{t^{\prime}=1}^{t} \frac{\partial \ell_{t}}{\partial h_{t}^{(i)}} \frac{\partial h_{t}^{(i)}}{\partial h_{t^{\prime}}^{(i)}} \frac{\partial h_{t^{\prime}}^{(i)}}{\partial u_{k i}}
$
이전 식에서 시점 t에서의 loss function에 관한 gradient로 일반화를 하기 위해서는 모든 시점에서의 gradient의 합으로 표현
$
\frac{\partial L}{\partial u_{k i}}=\sum_{t=1}^{T} \sum_{t^{\prime}=1}^{t} \frac{\partial \ell_{t}}{\partial h_{t}^{(i)}} \frac{\partial h_{t}^{(i)}}{\partial h_{t^{\prime}}^{(i)}} \frac{\partial h_{t^{\prime}}^{(i)}}{\partial u_{k i}}
$
$\frac{\partial h_{t}^{(i)}}{\partial h_{t^{\prime}}^{(i)}}$ 는 다음과 같이 나타낼 수 있다.
$
\frac{\partial h_{t}^{(i)}}{\partial h_{t^{\prime}}^{(i)}}=\prod_{g=t^{\prime}+1}^{t} \frac{\partial h_{g}^{(i)}}{\partial h_{g-1}^{(i)}}
$
이를 위 식에 대입하면 다음과 같은 수식을 얻을 수 있다
$
\frac{\partial L}{\partial u_{k i}}=\sum_{t=1}^{T} \sum_{t^{\prime}=1}^{t} \frac{\partial \ell_{t}}{\partial h_{t}^{(i)}}\left(\prod_{g=t^{\prime}+1}^{t} \frac{\partial h_{g}^{(i)}}{\partial h_{g-1}^{(i)}}\right) \frac{\bar{\partial} h_{t^{\prime}}^{(i)}}{\partial u_{k i}}
$
$W_{x h}$ 에 속하는 weight에 대해서도 유사한 방법으로 계산 가능
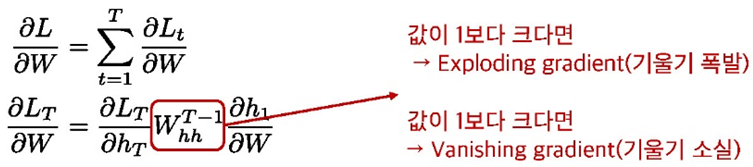
4.3.3 Problem of Vanilla RNN
● Short term memory 문제

● Non-linearity functions에 따른 문제

- sigmoid보다 derivative의 폭이 넓은 $\tanh$ 를 사용
- 그럼에도 $\tanh$ 의 값이 거의 항상 1 보다 작음 $\rightarrow$ Vanishing gradient(기울기 소실)
$$
\left.\frac{\partial L_{T}}{\partial W}=\frac{\partial L_{T}}{\partial h_{T}}\left(\prod_{t=2}^{T} \tanh ^{\prime}\left(W_{h h} h_{t-1}+W_{x h} x_{t}\right)\right)\right) W_{h h}^{T-1} \frac{\partial h_{1}}{\partial W}
$$
● 그렇다고 Non-linearity를 제거한다면,
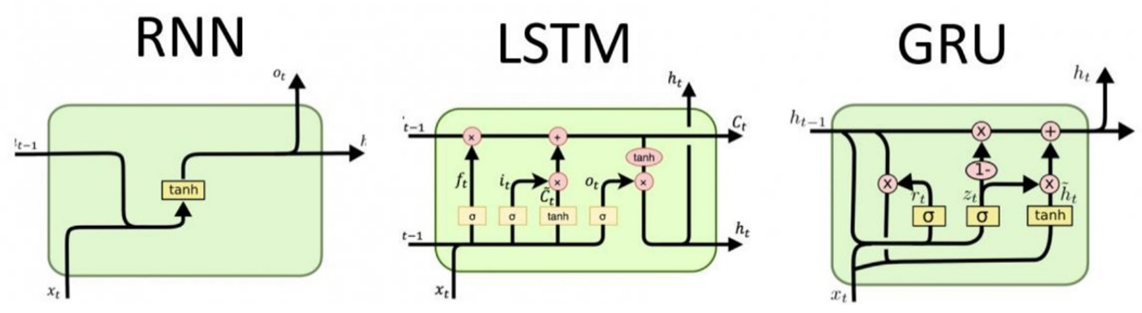
4.3.4 Solution to The Problem of Vanilla RNN
● Gate를 추가하여 선택적으로 정보를 기억할 수 있도록 개선
- Long Short Term Memory (LSTM) [Hochreiter, 1997], [Gers, 2000]
- Gated Recurrent Unit (GRU) [Cho, 2014]
'IT > 수업내용 정리' 카테고리의 다른 글
| ASR_Chpter 05: Sequence-to-Sequence with Attention (0) | 2024.10.28 |
|---|---|
| ASR_Chapter 3: Feed Forward Neural Net (0) | 2024.08.13 |
| pattern recognition_Ch 02 Bayesian Decision Theory (1) | 2022.12.21 |
| pattern recognition_ch01 Intro (0) | 2022.12.21 |
| ASR_Chapter 2: 입/출력 end 복잡도 분석 (0) | 2022.11.18 |



