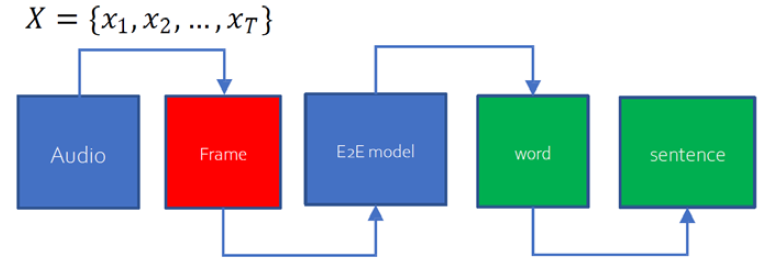
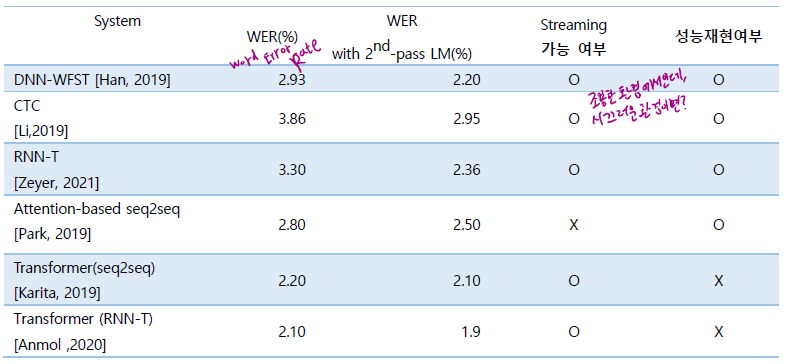
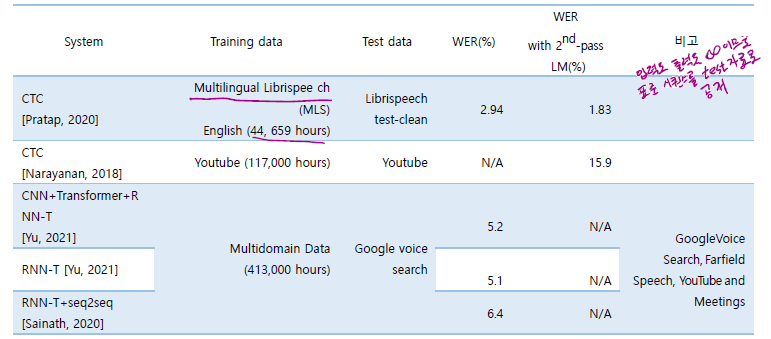
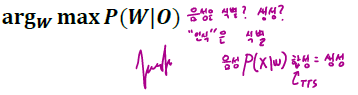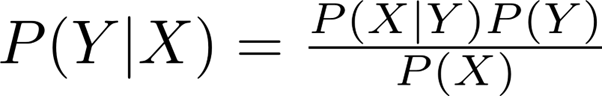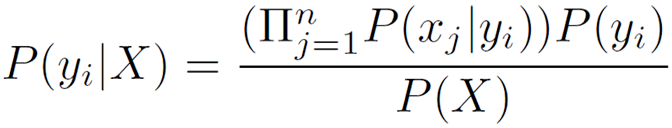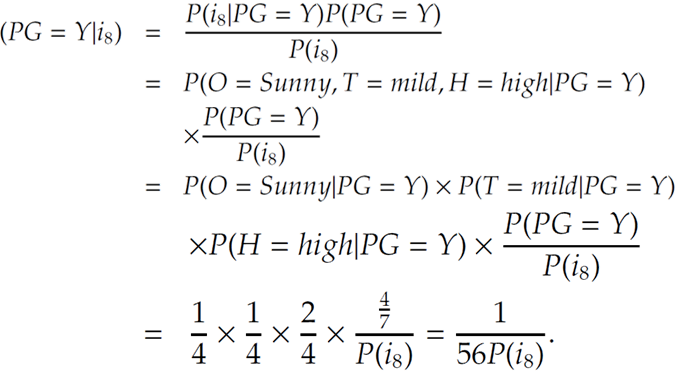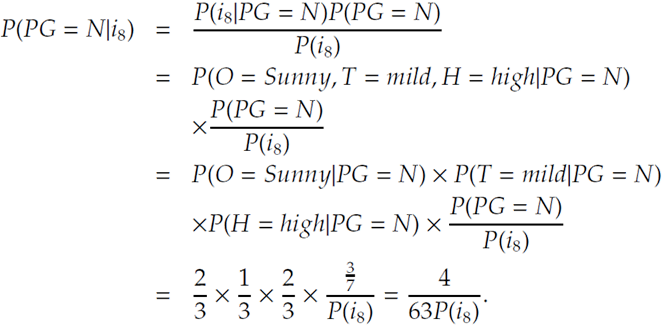Intreoduction

Bayesian Decision Theory

-       근본적인 통계 패턴 분류 문제에 대한 접근
-       다양한 분류간의 트레이드 오프를 정량화하는 것을 기반
-       확률을 이용한 결정과 그러한 결정에 수반되는 비용

State of nature ω  자연의 상태

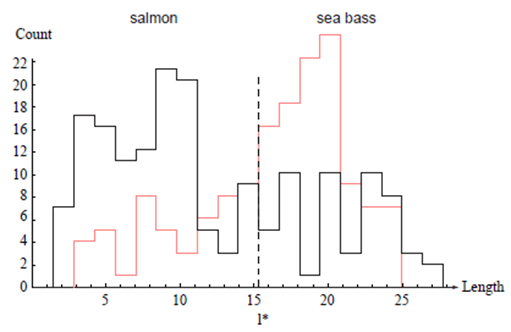
-        $\omega=\omega_1$ 을 위한 sea bass, $\omega=\omega_2$ 를 위한 salmon

-       자연의 상태는 예측불가
-       확률적으로 기술되어야 하는 변수

A priori probability

-       Seabass, salmon에 대한 사전지식의 반영

$P\left(\omega_1\right):$ Seabass일 사전확률

$P\left(\omega_2\right):$ Salmon일 사전확률

$P\left(\omega_1\right)+P\left(\omega_2\right)=1$ (단, 다른 생선이 없다면.)

Decision Rule

-       물고기를 보지 못하고 결정해야 한다면?
$P\left(\omega_1\right)>P\left(\omega_2\right)$ 면 $\omega_1$로 판정, 반대라면 반대로 판정

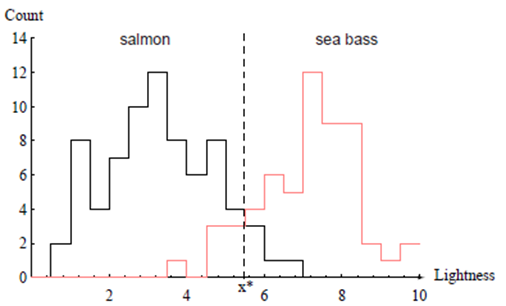
클레스-조건부(class-conditional)확률 밀도 함수 $p(x \mid \omega)$

-       자연의 상태가 ω  라고 주어졌을 때, x 에 대한 확률 밀도 함수

$p\left(x \mid \omega_1\right), p\left(x \mid \omega_2\right)$간의 차이는 Seabass와 Salmon의 모집단 간 밝기의 차이를 묘사

부류 $\omega_j$ 에 있고 특징 값x 를 갖는 패턴을 발견할 결합 확률 밀도는 두 가지 방법을 쓸 수 있다:

$p\left(\omega_j, x\right)=P\left(\omega_j \mid x\right) p(x)=p\left(x \mid \omega_j\right) P\left(\omega_j\right)$

Bayes formula

$P\left(\omega_j \mid x\right)=\frac{p\left(x \mid \omega_j\right) P\left(\omega_j\right)}{p(x)}$

이때 이 두부류의 경우는 $p(x)=\sum_{j=1}^2 p\left(x \mid \omega_j\right) P\left(\omega_j\right)$. posterior $=\frac{\text { likelihood } \times \text { prior }}{\text { evidence }}$

Bayes 공식은$x$ 의 값을 관찰함으로써 사전확률prior을 사후확률posterior(특징$x$ 가 측정되었을 때 자연 상태가$\omega_j$ 일 확률) 로 전환할 수 있다. $p\left(x \mid \omega_j\right)$는 $x$에 대한 $\omega_j$의 우도(likelihood)라고 부른다.

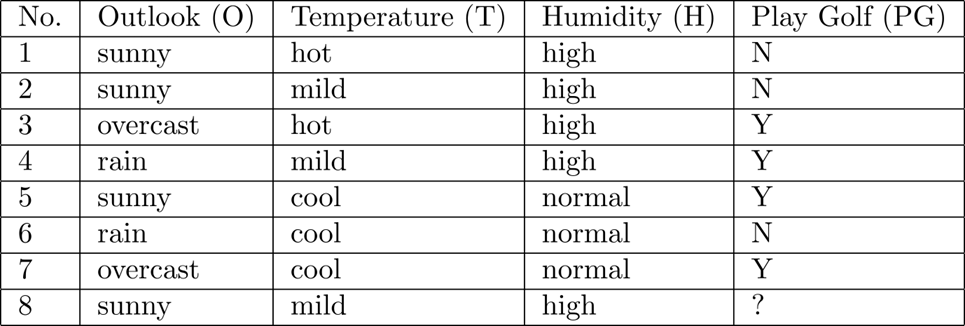
$P\left(\omega_1\right)=\frac{2}{3}$ and $P\left(\omega_2\right)=\frac{1}{3}$

Probability of error when decision is made

결정 방법은 $P($ error $\mid x)=\left\{\begin{array}{l}P\left(\omega_1 \mid x\right) * \text { if decide } \omega_2 \\ P\left(\omega_2 \mid x\right) * \text { if decide } \omega_1\end{array}\right.$

- 결정을 내릴 때 오류가 나올 확률은,$P($ error $)=\int_{-\infty}^{\infty} p($ error,$x) d x=\int_{-\infty}^{\infty} P($ error $\mid x) p(x) d x$ 만일 모든 x에 대해 $P(\operatorname{error} \mid x)$ 를 작게 만든다면 이 적분은 가능한 작아야 한다.

$P\left(\omega_j \mid x\right)=\frac{p\left(x \mid \omega_j\right) P\left(\omega_j\right)}{p(x)}$

Bayes Decision Rule (for minimizing the probability of error)

- Decide $\omega_1$ if $p\left(\omega_1 \mid x\right) P\left(\omega_1\right)>p\left(\omega_2 \mid x\right) P\left(\omega_2\right) ; \omega_2$ 로 판정 otherwise

- $\boldsymbol{p}(\boldsymbol{x})$ : 는 결정에 있어서는 크게 중요하지 않음 $\left(P\left(\omega_1 \mid x\right)+P\left(\omega_2 \mid x\right)=1\right)$

Decide $\omega_1$ if $p\left(\omega_1 \mid x\right) P\left(\omega_1\right)>p\left(\omega_2 \mid x\right) P\left(\omega_2\right) ; \omega_2$ 로 판정 otherwise

사후 확률의 역할을 강조.
- 만일 어떤 x에 대해서 $p\left(x \mid \omega_1\right)=p\left(x \mid \omega_2\right)$라면 판정은 전적으로 사전 확률에 의해 정해진다.
- $P\left(\omega_1\right)=P\left(\omega_2\right)$라면 판정은 전적으로 우도$p\left(x \mid \omega_j\right)$에 근거하게 된다.

Bayesion decion theory – continuious features(연속적 특징)

Bayesian Theory의 일반화

-       둘 이상(more than one feature)의 특징을 사용하는 것을 허용하는 것
- 스칼라 x

를 특징vector x

로 대체
- x

는 특징공간이라고 부르는 d

-차원 유클리드 공간 Rd

에 속함

Bayesion decion theory – continuious features(연속적 특징)

Bayesian Theory의 일반화

- 둘 이상(more than one feature)의 특징을 사용하는 것을 허용하는 것
- 스칼라 x 를 특징vector x 로 대체
- x 는 특징공간이라고 부르는 d-차원 유클리드 공간 $\mathbb{R}^d$ 에 속함

- 셋 이상(more than two states)의 자연의 상태를 허용하는 경우

- $\left\{\omega_1, \ldots, \omega_c\right\}: c$개의 자연의 상태(“categories”)의 유한 집합

- 분류 외의 행동을 허용하는 것

- $\left\{\alpha_1, \ldots, \alpha_a\right\}$: a개의 가능한 행동의 유한 집합

- 오류 확률(probability of error)보다 더 일반적이라 할 수 있는 손실 함수(loss function)를 도입.
  - 손실 함수는 각 행동의 비용을 정확하게 나타내며, 확률 측정을 판정으로 전환에 사용된다.
$\lambda\left(\alpha_i \mid \omega_j\right)$ : 자연의 상태가 $\alpha_i$ 일 때, $\omega_j$ 라는 행동을 취해서 초래되는 손실

$P\left(\omega_j \mid x\right)=\frac{p\left(x \mid \omega_j\right) P\left(\omega_j\right)}{{p(x)}}$ 이때, $\quad p(x)=\sum_{j=1}^c p\left(x \mid \omega_j\right) P\left(\omega_j\right)$

행동 $\alpha_i$를 취하는 것과 관련된 기대 손실은 단순하게 $R\left(\alpha_i \mid x\right)=\sum_{j=1}^c \lambda\left(\alpha_i \mid \omega_j\right) P\left(\omega_j \mid x\right)$

-       판정-이론 용어로는 기대 손실을 리스크라고 부르며, $R\left(\alpha_i \mid x\right)$ 를 조건부 리스크라고 부른다.

-      문제는 $P\left(\omega_j\right)$에 대해 전체적 리스크를 최소화하는 판정 룰을 찾는 것.

$R=\int R(\alpha(x) \mid x) p(x) d x \quad R$ : 최소화된 전체적 리스크

-      전체적 리스크를 최소화하기 위한 조건부 리스크 계산 $R\left(\alpha_i(x)\right)$ 가 가능한 작도록 $\alpha(x)$가 선택된다면 전체적 리스크는 최소화

$R\left(\alpha_i \mid x\right)=\sum_{j=1}^c \lambda\left(\alpha_i \mid \omega_j\right)\left(\omega_j \mid x\right)$

$i=1, \ldots, a$ 에 대해 계산하고, $R\left(\alpha_i \mid x\right)$ 가 최소인 행동 $\alpha_i$ 를 선택

Bayesion decion theory – 두 부류(Two-Category) 분류

-     $\alpha_1$:  자연의 참 상태가 $\omega_1$ 이라고 판정을 내리는 것

-     $\alpha_2$:  자연의 참 상태가 $\omega_2$ 이라고 판정을 내리는 것

-     $\lambda_{i j}=\lambda\left(\alpha_i \mid \omega_j\right)$: 자연의 참 상태가 $\omega_j$일 때 $\omega_i$라고 판정시 따르는 손실 이를 적용해서 $R\left(\alpha_i \mid x\right)=\sum_{j=1}^c \lambda\left(\alpha_i \mid \omega_j\right)\left(\omega_j \mid x\right)$ 를 다시 쓰면

-      조건부 리스크 $$
\begin{aligned}
& R\left(\alpha_1 \mid x\right)=\lambda_{11} P\left(\omega_1 \mid x\right)+\lambda_{12} P\left(\omega_2 \mid x\right) \\
& R\left(\alpha_2 \mid x\right)=\lambda_{21} P\left(\omega_1 \mid x\right)+\lambda_{22} P\left(\omega_2 \mid x\right)
\end{aligned}
$$
$\lambda_{11}, \lambda_{22}$ 는 잘한 것

-      최소 리스크 판정 룰을 표현하는 다양한 방법 
1. $R\left(\alpha_1 \mid x\right)<R\left(\alpha_2 \mid x\right)$ 이면 $\omega_1$ 로 판정
2. $\left(\lambda_{21}-\lambda_{11}\right) P\left(\omega_1 \mid x\right)>\left(\lambda_{12}-\lambda_{22}\right) P\left(\omega_2 \mid x\right)$ 일 때 $\omega_1$ 이라고 판정(사후확률로 표현)
3. $\left(\lambda_{21}-\lambda_{11}\right) p\left(x \mid \omega_1\right) P\left(\omega_1\right)>\left(\lambda_{12}-\lambda_{22}\right) p\left(x \mid \omega_2\right) P\left(\omega_2\right)$ 이면 $\omega_1$ 로 판정하고 아니면 $\omega_2$ 로 판정 (Bayes공식을 사용함으로 사후 확률을 사전 확률과 조건부 밀도로 대체)
4. $\lambda_{21}>\lambda_{11}$ 이라는 논리적 가정 하에서 만약 $\frac{p\left(x \mid \omega_1\right)}{p\left(x \mid \omega_2\right)}>\frac{\lambda_{12}-\lambda_{22}}{\lambda_{21}-\lambda_{11}} \frac{P\left(\omega_2\right)}{P\left(\omega_1\right)}$ 이면 $\omega_1$ 로 판정 

(Likelihood ratio: 이 형태의 판정 룰은 확률 밀도들의 $x$-종속성에 초점을 맞춘다. $p\left(x \mid \omega_j\right)$ 를 $\omega_j$ 의 함수(즉, 우도 함수)로 간주하고 우도 비 $\frac{p\left(x \mid \omega_1\right)}{p\left(x \mid \omega_2\right)}$ 를 만들 수 있다. 따라서 Bayes 판정 룰은 관찰 $x$ 에 독립적인 어떤 문턱 값을 우도비가 넘으면 $\omega_1$ 로 판정할 것을 요구하는 것으로 해석)

Bayesion decion theory – Minimum-error-rate Classification(최소 에러율 분류)

에러를 피하기 위해서는 자연의 상태와 차이가 가장 적은(오류를 최소화하는) 판정 룰을 찾는 것이 당연하다.

Zero-One loss function

$\lambda\left(\alpha_i \mid \omega_j\right)=\left\{\begin{array}{ll}0 & i=j \\ 1 & i \neq j\end{array} i, j=1, \ldots, c\right.$

-       옳은 판정에 대해서는 손실이 없음

-       모든 에러에 단위 손실을 부여

-       모든 에러는 같은 비용이 든다.

$\sum_{j=1}^c \lambda\left(\alpha_i \mid \omega_j\right) P\left(\omega_j \mid x\right)=\sum_{j \neq i} P\left(\omega_j \mid x\right)=1-P\left(\omega_i \mid x\right)$

조건부 리스크를 최소화하는 행동을 선택 if. $P\left(\omega_i \mid x\right)>P\left(\omega_j \mid x\right)$ we decide $\omega_i \forall j \neq i$

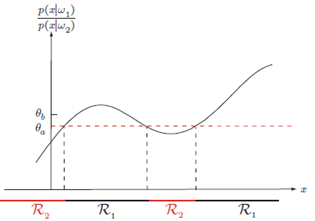
The likelihood ratio $p\left(x \mid \omega_1\right) / p\left(x \mid \omega_2\right)$

$\frac{p\left(x \mid \omega_1\right)}{p\left(x \mid \omega_2\right)}>\frac{\lambda_{12}-\lambda_{22}}{\lambda_{21}-\lambda_{11}} \frac{P\left(\omega_2\right)}{P\left(\omega_1\right)}$

Classifiers, Discriminant functions, and Decision surfaces

다분류 경우

패턴 분류기를 표현하는 다양한 방법중에 가장 쓸만한 방법중 하나
- 판별함수들$g_i(x), i=1, \ldots, c$ 에 의한 것

- 만일 $\boldsymbol{g}_{\boldsymbol{i}(\boldsymbol{x})}>\boldsymbol{g}_{\boldsymbol{j}}(\boldsymbol{x}) \forall \boldsymbol{j} \neq \boldsymbol{i}$ 이면 특징 벡터 $x$ 를 클레스 $\omega_i$ 에 할당한다.

분류기

-      분류기는 c개의 판별 함수를 계산하고 최대 판별식에 해당하는 부류를 선택하는 네트워크 또는 기계

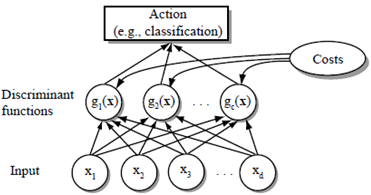
$g_i(x)=\left\{\begin{array}{c}g_1(x)=0.1 \\ g_2(x)=0.05 \\ \vdots \\ g_{n(x)}=0.85\end{array}\right.$ 중 가장 큰 것 선택

판별 함수들의 선택은 유일하지 않다.

$g_i(x)=-R\left(\alpha_i \mid x\right)$ (for risk)
$g_i(x)=P\left(\omega_i \mid x\right) \quad($ for minimum $-$ error $-$ rate $)$

판별함수의 수정이 가능

판정에 영향을 주지 않고 우리는 항상 모든 판별 함수들을 같은 양의 상수로 곱하거나 같은 상수를 더해서 이동시킬 수 있다. 더 일반적으로는 모든 $g_i(x)$ 를 단조증가함수 $f(\cdot)$ 에 의해 $f\left(g_i(x)\right)$ 로 대체시, 그로인한 분류는 변하지 않는다. 이것은 현저한 분석 및 계산 단순화로 이끌 수 있다.

$\left\{\begin{array}{l}g_i(x)=P\left(\omega_i \mid x\right)=\frac{p\left(x \mid \omega_i\right) P\left(\omega_i\right)}{\Sigma^c p\left(x \mid \omega_j\right)^{P\left(\omega_j\right)}} \\ g_i(x)=p\left(x \mid \omega_i\right) P\left(\omega_i\right) \\ g_i(x)=\ln p\left(x \mid \omega_i\right)+\ln P\left(\omega_i\right)\end{array}\right.$

모든 판정 룰의 효과는 특징 공간을 $c$ 개의 판정 영역 $\mathcal{R}_1, \ldots, \mathcal{R}_c$ 로 나누는 것 

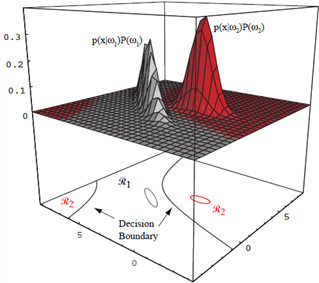
두 분류 경우

이분기(dichotomizer)
두 부류 경우는 다부류의 일종이나 정통적으로 독립해 다뤄왔다.
두 판별 함수 대신 단일 판별 함수를 정의하고 판정하는 것이 더 보편적이다.
$g(x) \equiv g_1(x)-g_2(x)$

$g(x)>0$ 이면 $\omega_1$, 아니면 $\omega_2$ 로 판정
$\boldsymbol{g}(\boldsymbol{x})=\boldsymbol{P}\left(\boldsymbol{\omega}_1 \mid \boldsymbol{x}\right)-\boldsymbol{P}\left(\boldsymbol{\omega}_2 \mid \boldsymbol{x}\right)$
$\boldsymbol{g}(\boldsymbol{x})=\ln \frac{\boldsymbol{p}\left(\boldsymbol{x} \mid \boldsymbol{\omega}_1\right)}{\boldsymbol{p}\left(\boldsymbol{x} \mid \boldsymbol{\omega}_2\right)}+\ln \frac{\boldsymbol{P}\left(\boldsymbol{\omega}_1\right)}{\boldsymbol{P}\left(\boldsymbol{\omega}_2\right)}$

The normal density

왜 Normal density인가?

-       분석의 용이함(해석학적으로 다루기 쉬움)으로, 다변량 normal밀도, 또는 Gaussian밀도는 많은 관심을 받았다.

-        중요한 상황에 적합한 모델. class $\omega_j$에 특징벡터 x가 단일 또는 프로토타입 벡터 $\mu_i$의 연속적 값을 가지고 랜덤하게 오염된 버전일 경우에 적합.

Expectation (expected value)
$$
E[f(x)]=\int_{-\infty}^{\infty} f(x) p(x) d x
$$
만약 특징 $\mathrm{x}$ 의 값들이 이산 집합 $\mathrm{D}$ 의 점이라면.
$$
E[f(x)]=\sum_{x \in D} f(x) P(x)
$$

The normal density – 단변량 밀도

$p(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left[-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2\right]$

- 평균
$$
\mu=E[x]=\int_{-\infty}^{\infty} x p(x) d x
$$
- 분산
$$
\begin{aligned}
& \sigma^2=E\left[(x-\mu)^2\right]=\int_{-\infty}^{\infty}(x-\mu)^2 p(x) d x \\
& -\quad \boldsymbol{p}(\boldsymbol{x}) \sim \boldsymbol{N}\left(\boldsymbol{\mu}, \boldsymbol{\sigma}^2\right)
\end{aligned}
$$
$x$ 는 평균 $\mu$ 와 분산 $\sigma^2$ 에 의해 분포된다.

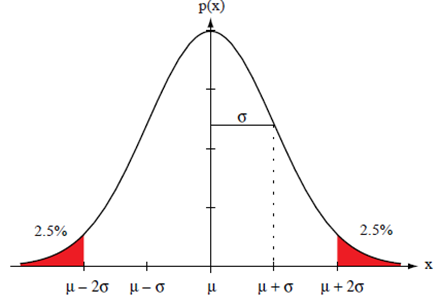
The normal density – 다변량 분포

$$
p(\boldsymbol{x}) \sim N(\boldsymbol{\mu}, \boldsymbol{\Sigma}) \quad p(\boldsymbol{x})=\frac{1}{(2 \pi)^{d / 2}|\boldsymbol{\Sigma}|^{1 / 2}} \exp \left[-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^t \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right]
$$
- 평균 벡터
$$
\text { - } \boldsymbol{\mu}=E[\boldsymbol{x}]=\int_{-\infty}^{\infty} \boldsymbol{x p}(x) d \boldsymbol{x}
$$
- 공분산 행렬 (Convariance)
$$
\Sigma=E\left[(\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^t\right]=\int_{-\infty}^{\infty}(\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^t p(x) d x{ }^*[x-\mu]=\left[\begin{array}{lll}
\sigma_{11} & & \\
& \ddots & \\
& \sigma_{n n}
\end{array}\right]
$$
- 통계적 독립성(statistical independence)
만약 $x_i$ 와 $x_j$ 가 통계적으로 독립적이면, $\sigma_{i j}=0$ 일 것이다. 만약 모든 비대각선 요소들이 0 이면, $p(x)$ 는 $x$ 의 요소들에 대한 단변량 노멀 밀도들의 곱으로 축소된다.

- 독립적이거나 아니거나, 결합적으로(jointly) 노멀하게 분포 하는 랜덤 변수들의 선형 결합(combination)은 노멀하게 분포한다.
$$
\begin{aligned}
& p(\boldsymbol{x}) \sim N(\boldsymbol{\mu}, \mathbf{\Sigma})  \\
& \boldsymbol{y}=\boldsymbol{A}^t \boldsymbol{x} \rightarrow p(\boldsymbol{y}) \sim N\left(\boldsymbol{A}^{\boldsymbol{t}} \boldsymbol{\mu}, \boldsymbol{A}^{\boldsymbol{t}} \boldsymbol{\Sigma} \boldsymbol{A}\right) \\
& * y=A^t y=\left[\begin{array}{lll}
y_1 \\
y_2
\end{array}\right]=\left[\begin{array}{ccc}
1 & \cdots & 0 \\
\vdots & A & \vdots \\
0 & \cdots & 1
\end{array}\right]\left[\begin{array}{l}
x_1 \\
x_2
\end{array}\right] 
\end{aligned}
$$
-임의의 다변량 분포를 구형(spherical)분포로 변환(공분산 행렬이 항등 행렬 $I$ 에 비례하는 분포)할 수 있다. (백색변환)
$$
A_\omega=\Phi \Lambda^{1 / 2} 
$$
$\boldsymbol{\Phi}$ : 열들이 $\Sigma$ 인 정규직교 고유 벡터들인 행렬
$\mathbf{\Lambda}$ : 해당 고윳값들의 대각선 행렬

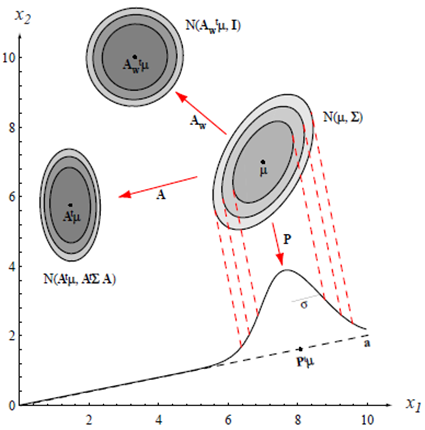
- 다변량 정규분포는 $\boldsymbol{d}+\boldsymbol{d}(\boldsymbol{d}+\mathbf{1}) / \mathbf{2}$ 개의 파라미터 즉, 평균 벡터 $\boldsymbol{\mu}$ 의 요소들과 공분산 행렬 $\boldsymbol{\Sigma}$ 에 의해 완전하게 정의된다.

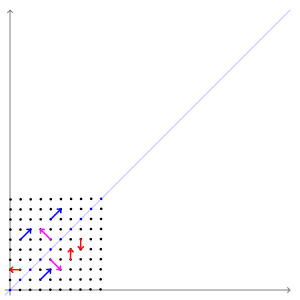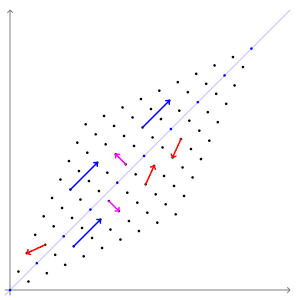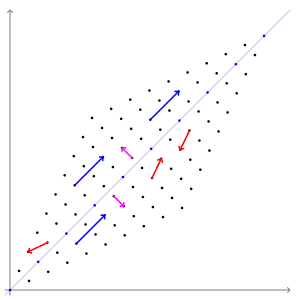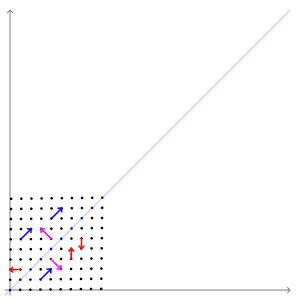
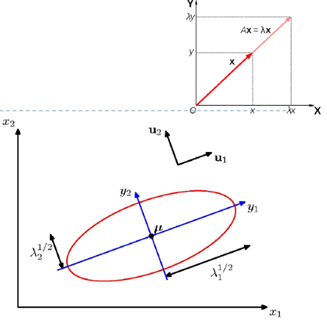
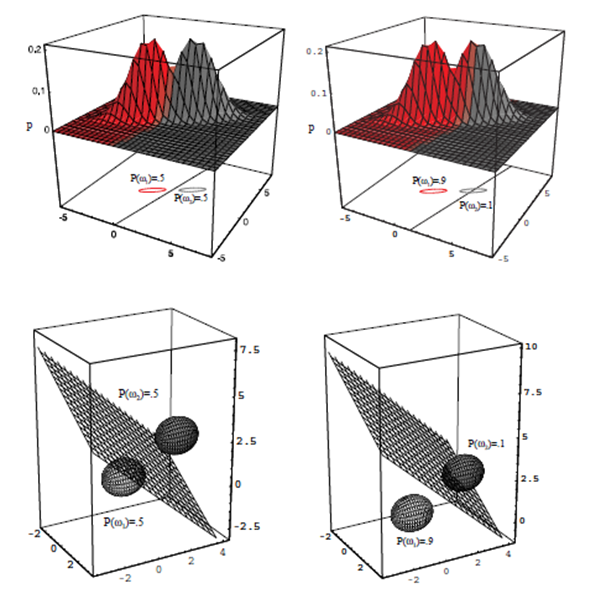
- 아래 그림에서:↓
- 클러스터의 중심은 평균 벡터에 의해 결정 
- 클러스터의 모양은 공분산 행렬에 의해 결정.
- 상수 밀도의 점들의 위치는 $(\boldsymbol{x}-\boldsymbol{\mu})^t \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})$ 가 상수 인 초타원체들이다
- 이 초타원체들의 주축은 $\Phi$ 에 의해 묘사되는 $\boldsymbol{\Sigma}$ 의 고유 벡터들에 의해 주어지며,  
고윳값들 $(\boldsymbol{\Lambda})$ 은 이 축들의 길이를 결정한다.
- Mahalanobis distance (from $x$ to $\boldsymbol{\mu}$ ) 마할라노비스 거리 $r^2=(\boldsymbol{x}-\boldsymbol{\mu})^t \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) 
(분산이 커지면, 거리는 작게 해석)

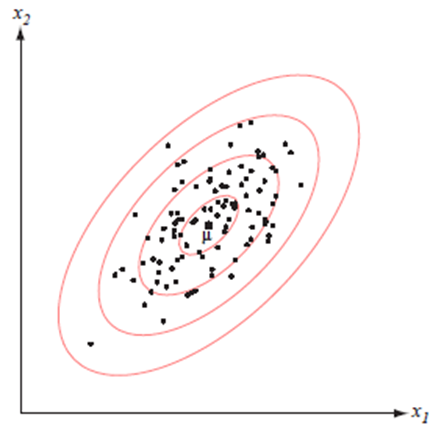
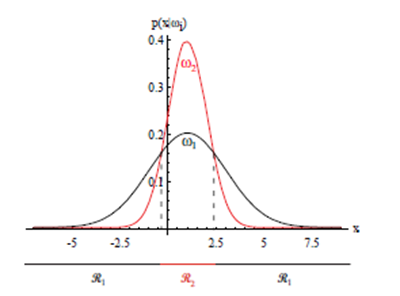
(PRML 2.3) The Gaussian Distribution

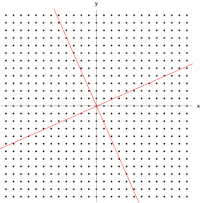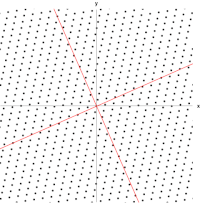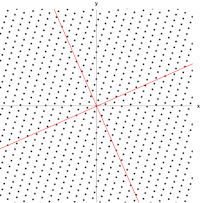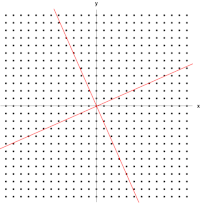
빨간색 선은 이차원 공간 $x=\left(x_1, x_2\right)$ 상에서의 상수 가우시안 확률 분포의 타원형 표면을 나타낸다. 여기서 말도는 $x=\mu$ 일 경우의 값의 $\exp (-1 / 2)$ 에 해당한다. 타원의 축들은 공분산 행렬의 고유 벡터들 $u_i$ 에 의해 정의 되 며, 각각의 축은 각각의 고윳값 $\lambda_i$ 에 대응된다.

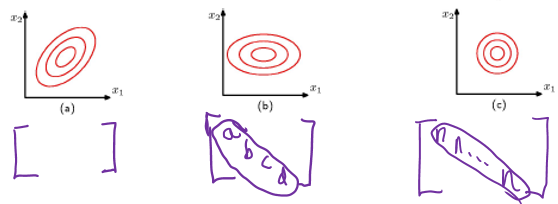
이차원 가우시안 분포에서의 상수확률 밀도의 경로.
(a)는 공분산 행렬의 형태가 일반적일 경우
(b)는 공분산 행렬이 대각 행렬인 형태
(c)는 공분산행렬이 항등행렬의 상수배일 경우이며 이 경우 경로가 동심원의 형태를 띈다.

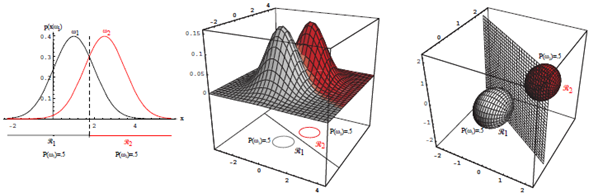
정규분포에 대한 판별 함수

- 최소 에러율 분류는 아래의 판별 함수로 달성될 수 있다.
$\begin{aligned} & p(\boldsymbol{x})= \frac{1}{(2 \pi)^{d / 2}|\boldsymbol{\Sigma}|^{1 / 2}} \exp \left[-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^t \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right] \text { 에 의해 } \\ & g_i(\boldsymbol{x})=-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)^t \boldsymbol{\Sigma}_i^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)-\frac{d}{2} \ln 2 \pi-\frac{1}{2} \ln \left|\boldsymbol{\Sigma}_i\right|+\ln P\left(\omega_i\right)\end{aligned}$

- 판별함수의 3가지 경우

1. $\boldsymbol{\Sigma}_i=\sigma^2 \mathbf{I}$
2. $\boldsymbol{\Sigma}_i=\boldsymbol{\Sigma}$
3. $\mathbf{\Sigma}_i=$ arbitrary

Case 1: $\Sigma_i=\sigma^2 I$

- 가장 간단한 경우
- 특징들이 통계적으로 독집적이고 각 특징이 같은 분산 $\sigma^2$를 가짐.
- 기하학적으로 샘플들이 같은 크기의 초구 클러스터에 놓이는 상황
-  $i$ 번째 클래스에 대한 클러스터는 평균 벡터 $\mu_i$ 가 중심으로 함.
- $\Sigma_{\mathrm{i}}$ 의 행렬식과 역의 계산이 쉬움 

$$
\left|\boldsymbol{\Sigma}_i\right|=\sigma^{2 d} \quad \boldsymbol{\Sigma}_i^{-1}=\frac{1}{\sigma^2} \mathbf{I}
$$

- $g_i(x)=-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)^t \boldsymbol{\Sigma}_i^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)-\frac{d}{2} \ln 2 \pi-\frac{1}{2} \ln \left|\boldsymbol{\Sigma}_i\right|+\ln P\left(\omega_i\right)$

$\boldsymbol{\Sigma}_i^{-1},\left|\boldsymbol{\Sigma}_i\right|, \ln 2 \pi$ 가 $i$ 에 대해 독립 
$$
\rightarrow g_i(x)=-\frac{\left\|x-\mu_i\right\|^2}{2 \sigma^2}+\ln P\left(\omega_i\right) 
$$
여기서 $\left\|x-\mu_i\right\|^2=\left(x-\mu_i\right)^t\left(x-\mu_i\right)$ 이며, 유클리드 놈을 나타냄.

- $g_i(\boldsymbol{x})=-\frac{1}{2 \sigma^2}\left[\boldsymbol{x}^t \boldsymbol{x}-2 \boldsymbol{\mu}_i^\tau \boldsymbol{x}+\boldsymbol{\mu}_i^\tau, \boldsymbol{\mu}_i\right]+\ln P\left(\omega_i\right)$
$g_i(x)=\boldsymbol{w}_{\boldsymbol{i}}^t \boldsymbol{x}+\omega_{i 0}$ 여기서 $w_i=\frac{1}{\sigma^2} \boldsymbol{\mu}_i$ and $\omega_{i 0}=\frac{-1}{2 \sigma^2} \boldsymbol{\mu}_i^t \boldsymbol{\mu}_i+\ln P\left(\omega_i\right)$

- 선형 식 $g_i(x)=g_j(x)$ 에 의해 정의되는 초평면들

$\mathbf{w}^t\left(\mathbf{x}-\mathbf{x}_0\right)$ 여기서 $\mathbf{w}=\boldsymbol{\mu}_i-\boldsymbol{\mu}_j$ and $\mathbf{x}_0=\frac{1}{2}\left(\boldsymbol{\mu}_i+\boldsymbol{\mu}_j\right)-\frac{\sigma^2}{\left\|\boldsymbol{\mu}_i-\boldsymbol{\mu}_j\right\|^2} \ln \frac{P\left(\omega_i\right)}{P\left(\omega_j\right)}\left(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j\right)$

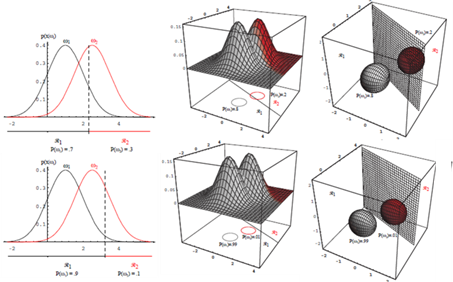
Case2: $\boldsymbol{\Sigma}_{\boldsymbol{i}}=\boldsymbol{\Sigma}$

- 모든 클래스의 공분산 행렬이 동일하다.
- 샘플들이 같은 크기와 모양의 초타원체 클러스터에 놓이는 상황에 해당
- $i$ 번째 클래스의 클러스터는 평균 벡터 $\boldsymbol{\mu}_i$ 를 중심으로 한다.

$g_i(x)=-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_{\boldsymbol{i}}\right)^t \boldsymbol{\Sigma}_i^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)-\frac{d}{2} \ln 2 \pi-\frac{1}{2} \ln \left|\boldsymbol{\Sigma}_i\right|+\ln P\left(\omega_i\right)$
$\frac{d}{2} \ln 2 \pi,\left|\boldsymbol{\Sigma}_i\right|$ 가 $i$ 에 대해 독립
$$
\rightarrow g_i(\boldsymbol{x})=-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)^t \boldsymbol{\Sigma}_i^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)-\ln P\left(\omega_i\right)
$$
- $i$ 에 독립적인 2차 항 $\boldsymbol{x}^t \boldsymbol{\Sigma}_i^{-1} \boldsymbol{x}$ 를 빼면,
$g_i(\boldsymbol{x})=\boldsymbol{w}_i \boldsymbol{x}+\omega_{i 0}$ 여기서 $\boldsymbol{w}_i=\boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}_i$ and $\omega_{i 0}=-\frac{1}{2} \boldsymbol{\mu}_i^t \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}_i+\ln P\left(\omega_i\right) $
이 판별식들은 선형적이므로 그로 인한 경계는 초평면이다. 이 초평면의 경계 식은.
$\boldsymbol{w}^t\left(\boldsymbol{x}-\boldsymbol{x}_0\right)=1$ where $\boldsymbol{w}_i=\boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}_i$ and $\boldsymbol{x}_0=\frac{1}{2}\left(\boldsymbol{\mu}_i+\boldsymbol{\mu}_j\right)-\frac{\ln \left[P\left(\omega_i\right) / P\left(\omega_j\right)\right]}{\left(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j\right)^t \boldsymbol{\Sigma}^{-1}\left(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j\right)}\left(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j\right)$
- $\boldsymbol{w}=\boldsymbol{\Sigma}^{-1}\left(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j\right)$ 는 일반적으로 $\boldsymbol{\mu}_i-\boldsymbol{\mu}_j$ 방향이 아니기 때문에 영역을 분리하는 초평면은 일반적으로 이 평균들을 잇는 선에 직교하지 않는다.

Case3: $\Sigma_i=\operatorname{arbitrary}($ (임의적)

- 일반적인 정규분포의 경우 공분산 행렬은 각 부류마다 다르다.
$$
\begin{aligned}
& g_i(x)=-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)^t \boldsymbol{\Sigma}_i^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)-\frac{d}{2} \ln 2 \pi-\frac{1}{2} \ln \left|\boldsymbol{\Sigma}_i\right|+\ln P\left(\omega_i\right) \\
& \frac{1}{2} \ln 2 \pi \text { 만이 i에 대해 독립 } \\
& \rightarrow g_i(\boldsymbol{x})=\boldsymbol{x}^t \boldsymbol{W}_i \boldsymbol{x}+\boldsymbol{w}_i^t \boldsymbol{x}+\omega_{i 0^2}  \\
& \text { where, } \boldsymbol{W}_i=-\frac{1}{2} \boldsymbol{\Sigma}_i^{-1}, \boldsymbol{w}_i=\boldsymbol{\Sigma}_i^{-1} \boldsymbol{\mu}_i \text { and }  \\
& \omega_{i 0}=-\frac{1}{2} \boldsymbol{\mu}_i^t \boldsymbol{\Sigma}_i^{-1} \boldsymbol{\mu}_i-\frac{1}{2} \ln \left|\boldsymbol{\Sigma}_i\right|+\ln P\left(\omega_i\right) 
\end{aligned}
$$

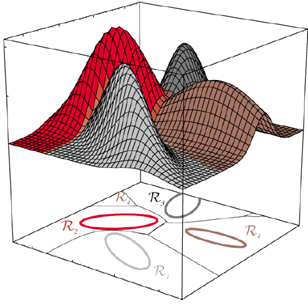
EXAMPLE1: 2차원 가우스 데이터에 대한 판정 영역

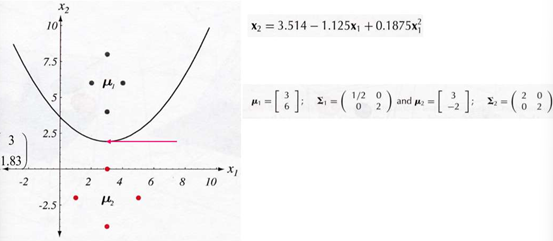
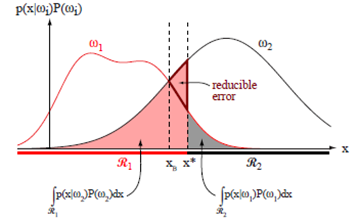
정규 분포의 오차 범위

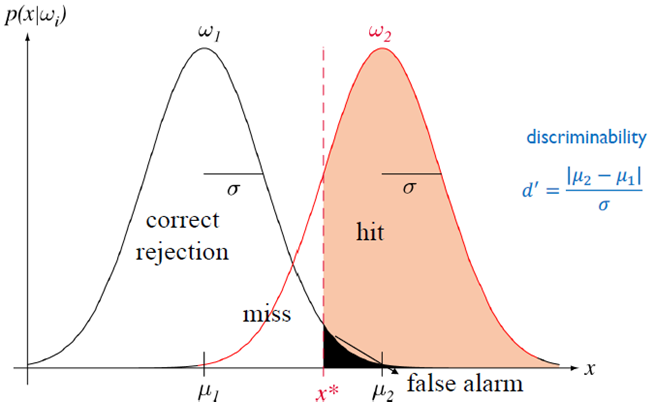
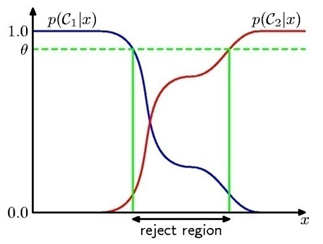
ROC(receiver operation characteristic)(수신기 동작 특성)

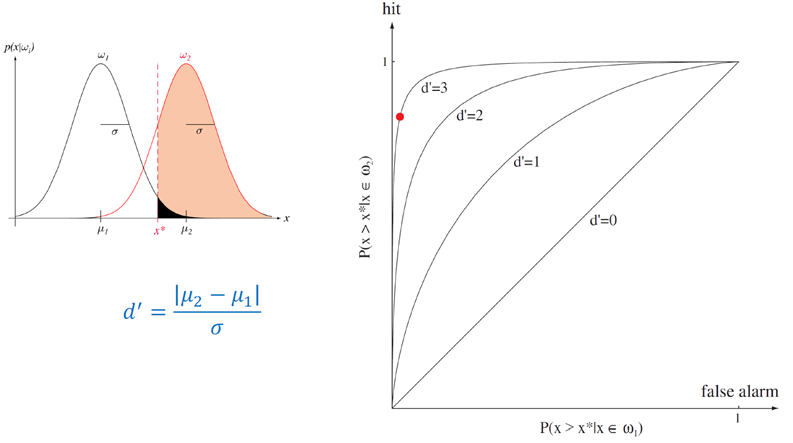
Bayes decision theory-이산적 특징

- 많은 실제 응용에서 구성요소 (특징벡터) x 는 2진, 3진, 또는 더 높은 진수의 정수값을 가지고, $x$ 는 $m$ 개의 이산 값 $v_1, \ldots, v_m$ 중 하나만 취할 수 있다.
$$
\int p\left(x \mid \omega_j\right) d x \rightarrow \sum_x P\left(x \mid \omega_j\right)
$$

- bayes 공식은 확률 밀도가 아닌 확률들을 포함

$$
P\left(\omega_j \mid x\right)=\frac{P\left(x \mid \omega_j\right) P\left(\omega_j\right)}{P(x)} \quad P(x)=\sum_{j=1}^c P\left(x \mid \omega_j\right) P\left(\omega_j\right)
$$

- 조건부 리스크 $R(\alpha \mid x)$ 의 정의는 변하지 않으며, bayes판정 룰도 동일하다.
- 사후 확률을 최대화하여 오류율을 최소화하는 기본 룰도 바뀌지 않는다.

독립적 2진 특징

- 특징 벡터의 요소들이 2진 값이고, 조건부 독립인 2부류 문제를 고려
$$
\begin{aligned}
& \text { Let } x=\left(x_1, \ldots, x_d\right)^t \text { 여기서 요소 } x_i \text { 는 } 0 \text { 또는 } 1 \text { 로 놓고 확률들은 다음과 같다. } \\
& p_i=\operatorname{Pr}\left[x_i=1 \mid \omega_1\right] \text { and } q_i=\operatorname{Pr}\left[x_i=1 \mid \omega_2\right] \\
& \rightarrow P\left(x \mid \omega_1\right)=\prod_{i=1}^d p_i^{x_i}\left(1-p_i\right)^{1-x_i} \text { and } P\left(x \mid \omega_2\right)=\prod_{i=1}^d q_i^{x_i}\left(1-q_i\right)^{1-x_i} \\
&
\end{aligned}
$$
그럼 우도비는
$$
\frac{P\left(x \mid \omega_1\right)}{P\left(x \mid \omega_2\right)}=\prod_{i=1}^d\left(\frac{p_i}{q_i}\right)^{x_i}\left(\frac{1-p_i}{1-q_i}\right)^{1-x_i}
$$

$$
\begin{aligned}
& \text { - 판별함수 }\left(g(x)=P\left(\omega_1 \mid x\right)-P\left(\omega_2 \mid x\right)-(30), g(x)=\ln \frac{p\left(x \mid \omega_1\right)}{p\left(x \mid \omega_2\right)}+\ln \frac{P\left(\omega_1\right)}{P\left(\omega_2\right)}-(31)\right. \text { 로 부터) } \\
& g(x)=\sum_{i=1}^d\left[x_i \ln \frac{p_i}{q_i}+\left(1-x_i\right) \ln \frac{1-p_i}{1-q_i}\right]+\ln \frac{P\left(\omega_1\right)}{P\left(\omega_2\right)}
\end{aligned}
$$
- 이 판별 함수는 $x_i$ 에서 선형적이다. 따라서...
$$
\begin{aligned}
g(\boldsymbol{x}) & =\sum_{i=1}^d \omega_i x_i+\omega_0  \\
\text { 여기서 } \omega_i=\ln \frac{p_i\left(1-q_i\right)}{q_i\left(1-p_i\right)} \quad i=1, \ldots, d \quad & \omega_0=\sum_{i=1}^d \ln \frac{1-p_i}{1-q_i}+\ln \left(\frac{P\left(\omega_1\right)}{P\left(\omega_2\right)}\right)
\end{aligned}
$$

CH01 intro

1.1 기계인지

패턴을 인식은 음성인식, 지문식별, OCR, DNA시퀀스 식별 등 많은 곳에서 유용하다.

패턴인식의 방법론은 자연계, 특히 인간의 패턴 인식 체계에 대해 실제로 자연계가 이 문제를 어떻게 푸는가에 대한 지식에 영향을 받아 이뤄진다.

1.2 보기

예를 들어 생선 통조림 공장에서 생선을 분류하는 과정을 자동화하기를 원한다고 하자.
생선은 컨베이어 벨트에 실려 지나가며, 광학 센서를 이용해서 Sea bass salmon을 분류할 것이며, 카메라를 설치하여 sample 영상을 얻어 두 어종간의 외형적 차이(길이, 밝기, 폭, 지느러미 수와 모양, 입의 위치 등)을 적다보면, 이중 분류기에 사용할 특징이 나올 것이다.
이때, 영상의 노이즈, 또는 변화(밝기, 컨베이어위의 위치,. 잡영(static))도 주목해야 할 것이다.

Sea bass와 Salmon의 모집단 간에 차이가 있다는 사실이 주어지면, 이들을 (보통 수학적 형태인 다른 묘사들)모델로 본다.

Pattern classification에서 전체를 지배하는 목표와 방식은 이 모델들의 class를 가정하고, 감지된 data를 처리해서 노이즈를 제거한 뒤, 감지된 모든 pattern에 대해 가장 잘 일치하는 모델을 선택하는 것이다.
전처리 과정에서는 segmentation 연산이 가능한데, 이때, 배경분리, 서로간에 분리가 이뤄진다.

이후 그 정보들이 Feature 추출기로 가면, 어떤 특징, 특성을 측정해서 데이터를 축소한다.

이 값들이 분류기도 가면, 이것들을 평가하고, 최종적으로 어종에 대한 판정을 내린다.

그렇다면 이 특징 추출기와 분류기가 어떻게 설계될 것인가를 고려하자면, 누군가가 Sea bass가 Salmon보다 더 길다고 정보를 알려줬다면, 이 사실은 이 어류에 대한 모델을 제공한 것이다.

모델: Seabass는 어떤 전형적 길이를 가지고, 그 길이는 Salmon보다 크다. 따라서 길이는 분명한 특징이 되며, 생선의 길이 $ l $을 통해 분류를 시도할 수 있을 것이다.

이를 위해 sample을 얻고 측정하고 결과들을 살펴보면 그림 1.2와 같다.

그림 1.2에서는 Seabass가 Salmon보다 다소 긴 것을 알려주지만, 사실 신뢰성은 떨어진다.

이번엔, 그림 1.3과 같이 밝기로 시험을 해보니, 상당히 만족스럽게 나옴을 알 수 있다.

다만, 이제까지 분류의 결과들은 비용이 같다고 가정되었다. 예를들어 Salmon을 Seabass로 판정하는 것과 그 역이 동일하다는 것.
하지만, Seamon을 샀는데 Seabass가 들었다면 더 강력한 항의가 있을 것이기에 이 비용은 현실적에서는 맞지 않다.

따라서 decision boundary를 왼쪽으로 더 이동시켜 Salmon으로 분류되는 Seabass의 수를 줄여야 한다. 이는 비용에 따라 더 왼쪽으로 이동할 수도, 오른쪽으로 이동할 수도 있다.
본질적으로 이러한 비용을 최소화하도록 판정경계를 나누는 것이 decision theory의 핵심이다.

판정과 관련된 비용을 알고 있어 최적의 기준 값 x*을 선택했다 해도, 결과가 만족스럽지 않다면, 더 나은 성능을 제공할 방법을 찾아야 한다. 즉, 여러 특징에 의존하게 된다.

이번엔, Seabass가 일반적으로 Salmon보다 폭이 더 넓다는 사실을 이용해보자.
밝기 $x_1$ 과 폭 $x_2$ 를 2차원 특징 공간의 점 또는 vector x로 축소시킨다. $x=\left(\begin{array}{l}x_1 \\ x_2\end{array}\right)$

이제 문제는 이 특징공간을 두 영역으로 나누는 것이고, 한 영역의 모든 점은 Seabass, 다른 영역은 Salmon이 될 것이다.
sample에서 그림 1.4의 분포를 얻었다고 하자.

이 결과를 보면, 더 많은 특징을 사용하는 것이 꽤나 바람직하다. 이외에도 등지느러미의 꼭대기 각도, 눈의 배치(입-꼬리까지의 거리에 대한 비)같은 특징을 포함시킬 수 있을 것이다.
다만, 이 특징들은 중복될 수도 있고, 어떤 특징은 성능향상이 없을수도 있으며, 차원의 저주를 야기할 수 있다. 또한 측정 비용도 무시못할 요소이다.

그래서 두 특징들에 판정을 내리도록 강요된다 가정해보자. 만약 모델이 너무 복잡하다면, 그림1.5와 같은 복잡한 판정경계를 갖는다.

이 경우 sample은 완벽히 분류하겠지만 새로운 패턴에는 정확도가 떨어질 것이다. 이것이 일반화(General-Ization)에 대한 이슈이다.
사실상 그림 1.5는 특정 패턴에 과적합 되어 있다. 해결방법은 더 많은 학습 샘플을 구하는 것이지만, 이게 어려울 때는 다른 방법을 사용해야 한다.
그렇기에 실제 자연은 복잡한 판정경계가 아닐 것이라는 확신을 가지고 단순화한 것이 그림 1.6이다.

 이 경우 새로운 데이터에 더 좋은 결과를 보인다면, sample에 대해 조금 저조해도 만족할 수 있을 것이다. 하지만, 더 간단한 분류기가 좋다는 것을 어떻게 뒷받침할까?
 그림 1.4가 1.5보다 좋다고 말할 수 있는가? 이 절충관계를 어떻게든 최적화할 수 있다고 가정하면, 시스템이 모델을 얼마나 잘 일반화할 수 있을것인지를 예측할 수 있는가? 이것이 바로 통계적 패턴 인식의 핵심 문제에 속한다.

우리의 판정은 특정 작업, 비용을 위한 것이며, 범용성을 가지에 만든다는 것은 어려운 도전이다.
기본적으로 분류는 그 패턴들을 만든 모델을 복구하는 작업이기에, 모델의 유형에 따라 분류 기법은 달라질 수 있다.
이러한 기법은 NeuralNet, 통계적 인식, 구문론적 패턴 인식 등 다양한 방법이 있다.
다만 거이 모든 문제에서의 중점은 구성성분간 구조적 관계가 간단하고 자연스레 드러나며, 패턴의 전형적 모델이 나타내질 수 있는 좋은 표현을 달성하는 것이다.
경우에 따라 패턴들은 실수값의 vector, 정렬된 속성, 관계에 대한 표사로 표현될 것인데, 어쨌든 비슷한 애들끼리는 서로 가까이 있고, 다른 애들끼리는 멀리 있게 되는 표현을 찾는 문제라 할 수 있다.

reference: 김경환 교수님 패턴인식 강의, duda pattern recognition

Chapter 2: 입/출력 end 복잡도 분석

Table of contents

2.1음성 신호 저장 방법 및 시스템 입력

2.2음성 출력 단위 결정

2.1 음성 신호 저장 방법 및 시스템 입력

§  음성 신호의 저장 방법 (sampling rate: 16K, PCM)

§  음성 신호 저장 시 필요한 parameter (PCM, Pulse-Code Modulation 기준)

•           Sampling rate
⁻ 단위 시간당(초당) sampling의 횟수
⁻ Nyquist theorem
   ⁎ Sampling rate의 절반의 해당하는 주파수 대역까지 복원 가능함
⁻ Sampling rate는 음질을 결정한다.
   ⁎ 음악 저장에 많이 사용되는 sampling rate은 초당 44.1k(cd)
      • 사람의 가청 주파수 대역은 일반적으로 20Hz~20kHz로 알려져 있음
   ⁎ 전화의 sampling rate : 초당 8k
   ⁎ 현재 음성 인식에 많이 사용 되는 sampling rate는 초당 16k임

•           Sample 당 byte수
⁻ Sample당 2byte 사용 (216 = 65,536 )

§  음성 신호의 저장 방법(예제)

•           가수가 10곡을 수록한 앨범을 발매했다. 이를 CD에 담았을 때, 전체 CD 중 burning된 부분은 CD 전체 면적의 몇 %인가?
⁻ 한 곡의 길이는 4분으로 가정
⁻ CD는 총 700MB를 저장한다고 가정
⁻ Sampling rate: 초당 44,100
⁻ Sample당 2byte 사용
⁻ Stereo로 녹음되었기 때문에 채널은 2개

⁻ 44,100(samples/sec) * 2(bytes) * 240(secs) * 10(곡) * 2(channels) = 423,360,000
  ⁎ 답 : 423.36/700 MB, 60.48%

§   음성인터페이스의 가능한 입력 개수 분석(계속)

•           정량적 분석
⁻ 가정 : 입력 길이 1초, sampling rate 44.1k, sample당 2B사용
⁻ 저장에 1 * 44100 * 2 = 88,200B 필요
⁻ 가능한 입력의 개수: 288200∗8
⁻ 입력 길이의 제한이 없으므로 가능한 입력의 개수: 무한대

§  용량을 최대한 줄이면서, 음성 인식에 유용한 정보는 최대한 유지하는 feature추출이 필요

•           전체 음성을 20ms단위의 window로 나누고, 각 window별로 13차 MFCC feature를 추출하여 사용함

§  왜 window별로 feature를 추출하는가?

•           Feature추출이 가능 하려면, modeling과 분석이 가능해야 함

•           현재까지의 발화를 바탕으로 미래의 발화를 예측할 수 있는가?
⁻ 화자가 발화를 중지할 수 도 있고, 발화의 내용을 갑자기 바꿀 수 있음 따라서, 예측 가능하지 않음
⁻ 예측 가능하지 않다면, modeling과 분석이 불가능함

•           사람의 성대를 하나의 발성 기관으로 본다면, 발성 기관의 물리적 한계(제약)로 인하여 어떠한 짧은 시간에 대하여 미래의 발화를 예측할 수 있음
⁻ 음성은 quasi-stationary함 (짧은 구간에서만)
⁻ 다양한 실험을 바탕으로 window의 길이는 20ms로 도출됨

§  음성 신호를 short integer type의 2차원 array로 저장함

•           하나의 window에는 320개의 sample이 들어감

•           2byte(short integer)형식의 2차원 array로 저장
⁻ C 언어에서는 short[T][320]의 형태로 표현됨

§  MFCC feature 추출 과정

§  Fast Fourier Transform(FFT)

•           기본 가정:
⁻ 모든 주기적인 신호는 정현파(ex> sin, cos)의 합으로 나타낼 수 있다
⁻ 모든 신호를 𝛼 ∗ sin 𝛽 ∗ 𝜋의 합의 형태로 표현 가능

§  Time domain의 data를 frequency domain의 data로 변형

⁻ Frequency domain으로 나타내어진 결과를 spectrum이라고 함

§  예제

•           음성 신호에서 fundamental frequency를 정의하려면?
⁻ 일반적으로 사용하는 16kHz sampling rate의 경우, 8kHz까지 복원 가능함
⁻ FFT 분석을 위해 8kHz를 일정 크기로 분리 (fft size: $2^10$ 개)
⁻ FFT 분석에는 복소수가 사용되는데, 실수와 허수의 벡터 성분이 대칭을 이루기 때문에
  중복되는 값을 버리고 실수 값만을 사용
⁎ (fft size/2 = $2^9$ 개)
⁻ fundamental frequency : 8000/512 = 15.625Hz
⁻ 음성 신호에서의 frequency는 15.625의 배수로 나타냄

§  예제

•           3125Hz, 6250Hz의 frequency를 가진 sine wave를 중첩 시킨 pcm

•           Time과 frequency domain을 각 축으로 표현하고, amplitude를 색으로 표현한 것을 spectrogram이라 함

•           FFT를 통해 음성 신호의 특징을 표현할 수 있음

§  음소별로 spectrum의 모양이 다름

§  Mel-filterbank & Log

•           x(n) = v(n)*e(n) 을 음성이라고 가정
⁻ v(n) = 구강구조
⁻ e(n) = 성대에서 울리는 소리

•           v(n)은 음성에 대한 정보
⁻ 무슨 말을 했는지에 대한 정보

•           e(n)은 화자에 대한 정보
⁻ 어떤 사람이 말을 했는지에 대한 정보

•           x(n) = v(n)*e(n) 이 마이크를 통해 입력됨
⁻ Time domain

•          FFT를 통해 frequency domain으로 변환

⁻ convolution이 곱셈으로 변환

•           X(n)에서 화자 정보인 e(n)을 제거하기 위해 log를 씌워 덧셈으로 변환
⁻ Log(X(n)) = Log(V(n)) + Log(E(n))

§  Discrete Cosine Transform(DCT)

•           적은 차원의 데이터로 envelop을 구할 때 사용됨

•           Discrete Cosine Transform(DCT) 과정을 통해 음성 인식에 있어 필요한 정보만을 담은 13차 vector를 생성

§  MFCC feature 추출 과정

2.2음성 출력 단위 결정

§  각 단어들은 컴퓨터 내부에서 어휘에 대한 index로 표현

•           어휘(Vocabulary): 인식 가능한 단어들의 집합

•           예: 어휘의 크기가 10만이고, 단어들은 어절단위로 구분 되었으며, 어휘 내 단어들을 가나다순으로 정렬했 을 때, 단어들이 아래의 순서의 단어로 어휘 내 위치해 있다고 가정한다.
⁻ ‘가자’: 12,844번째 단어
⁻ ‘내일’: 24,882번째 단어
⁻ ‘세시에’: 35,493번째 단어
⁻ ‘오후’: 69,864번째 단어
⁻ ‘학교’: 95,867번째 단어

•           ‘내일/오후/세시에/학교/가자’는 아래와 같이 index의 열로 표현된다.
⁻ 24,882/69,864/35,493/95,867/12,844

§  한국어 문장 예제: (형태소 단위로 시퀀스를 구성)

•           올 여름 평년보다 덥고 강수량 지역 차 크다
⁻ <s>/올/여름/평년/보다/덥/고/강수량/지역/차/크/다/</s>
⁻ w0/w1/w2/w3/w4/w5/w6/w7/w8/w9/w10/w11/</s>

§  영어 문장 예제: (단어 단위로 시퀀스를 구성)

•           It is hotter than usual this summer, and the regional difference of precipitation is big
⁻ <s>/It/is/hotter/than/usual/this/summer,/and/the/regional/difference/of/precipitation/is/big/</s> (<s>와 </s>는 각각 start, end를 나타내는 정의)
⁻ w0/w1/w2/w3/w4/w5/w6/w7/w8/w9/w10/w11/w12/w13/w14/w15/w16

reference: 서강대 김지환 교수님 강의

Chapter 1: 음성인식 연구 동향 및 문제 정의

Table of contents

1.1 음성인식 문제 정의

1.2 음성인식 연구 동향

1.1 음성인식 이란?

v  마이크를 통해 입력 받은 음성(speech)이 주어졌을때, 확률이 가장 높은 문장(단어의 열)을 출력

v                  

•       $W=\left\{w_1, w_2, \ldots, w_U\right\}$ : U개의 단어 시퀀스

•       $X=\left\{x_1, x_2, \ldots, x_r\right\}$ : 음성 시퀀스

1.1 E2E 관점의 음성인식 문제정의

 음성인식을 입력end (음성)에서 출력end (문장)으로의 변환의 문제로 본다면

  음성인식문제는

•   $x_1 \cdots x_r$ (Continuous vector space에서의 13차 벡터 𝑇개의 시퀀스)에서
     $w_1, \cdots, w_U$(𝑉개의 서로 다른 값을 가지는 discrete symbol𝑈개의 시퀀스)로의 번역 문제로 재정의 할 수 있다

이상적인 E2E 시스템 구현은 불가능

이상적인 E2E시스템: 전체 시스템을 블랙박스로 보고 데이터만 주면 알아서 시스템이 학습하는방식

•   무한개의 입력 시퀀스에서 무한개의 출력 시퀀스로 매핑하는 시스템은 구현이 불가능하다

1.1 E2E 음성인식 구현 시 입출력 복잡도

음성인식 시스템의 가능한 입력 개수 분석

•   가정: 입력 길이 1초, 44.1K, 샘플 당 2byte 사용

•   저장에 1 × 44100 × 2 = 88,200 byte 필요

•   가능한 입력의 개수: 288200 × 8

•   입력 길이의 제한이 없으므로 가능한 입력의 개수는 무한대이다

음성인식 시스템의 가능한 출력 개수 분석

•   어휘를 구성하는 단어의 수(𝑉) : 무한대 (지명, 인명 등 제한이 없으며 신조어가 계속해서 생성된다)

•   연속음성인식에서는 입력 파형만을 가지고 몇 개의 단어로 구성된 문장인지 알수 없다

1.1 DNN-WFST에서의 문제 정의

기호 설명

•           $W: w_1 \cdots w_N$
- N개의 단어들로 이루어진 문장

•           $O: o_1 \cdots o_T$
⁻ T개의 윈도우에서 각 윈도우로부터 나온 13차 vector의 sequence(.$ x: x_1, x_2, ..., x_t$ )

가능한 O 의 개수가 무한대이기 때문에 P(W | O) 를 직접 구할 수 없음

Bayesian rule을 적용하여 변환

$$
\arg _w \max P(W \mid O)=\arg _w \max \frac{P(O \mid W) P(W)}{P(O)}
$$

•        P(O) : 13 * T  벡터 공간에서의 한 점의 확률

•        이 확률을 모두 동일하다고 가정하면 $\arg _w \max$ 를 찾는 문제이기 때문에 P(O) 를 생략 가능

                                            
                           

음성인식 시스템 구성에서의 핵심

•        음향 모델P(O | W)

•        언어 모델P(W)

•        디코딩 네트워크($\arg _w \max$)

•           어휘(인식 가능한 단어 set)의 구현이다

 

1.2   주요 음성인식 모델

DNN-WFST

- Kaldi(음성인식 주요 tool)의 기반
- E2E에 대응되는 기술로 서술되나,
  Frame 단위까지(출력 end가 HMM에서의 state)의 E2E임

E2E (출력 end는 주로 grapheme)

- CTC
- RNN-T
- Attention
- Transformer

1.2 E2E방법의 장점 및 주요 검토 항목

장점

•           SOTA(State-of-the-art)를 보임 (transformer)

•           음성파일과 이에 대응되는 transcription만으로 학습

•           전혀 모르는 언어에 대해서도 음성인식기 제작이 가능

단점

•           외부 지식을 실시간 반영할 수 있는 방법이 없음 (예: 실시간 검색어(고유명사 많음))

•           대용량 텍스트 코퍼스를 음성인식기에 직접 반영할 수 있는 방법이 없음

•           복잡한 구조에 파라미터가 많고, computation power를 많이 사용하며, ML 기반으로 학습이 이루어짐 (입력열과는  다른 길이를 가지는 출력열에 대한답만 가지고 있음)

•           재현 실험이 되지 않는 경우가 많음 (모델 초기값에 의해 성능이 바뀔 수 있음)

주요검토항목

•           DNN-WFST 대비 성능이 좋은가?

•           재현 실험은 잘이루어 지는가?

•           필요한 computation power는?

•           출력 단위 정의

1.2 주요 E2E 방법

End-to-end models

•           Connectionist temporal classification (CTC) [Graves, 2006]

-  알파벳과 음성정보만으로 단일모델을 구성할수 있는, 최초로 제안된 end-to-end 음성인식모델

•           RNN-transducer (RNN-T) [Graves, 2012]

-  CTC에 언어 정보를 학습할 수 있는RNN 기반의 모델을 추가하여 성능을 개선시킨 모델

•           Attention 기반 seq2seq [Chan, 2016]

-  음성인식을sequence의 번역으로 해석해서attention mechanism을적용한모델

•           Transformer [Vaswani, 2017]

-  Multi-head self-attention을 사용하여 RNN 없이 sequence 모델링을 구현한 모델

Librispeech corpus 대상 end-to-end 음성인식 모델 성능 비교

대용량 corpus 대상 end-to-end 음성인식 모델 성능

reference:서강대학교 김지환 교수님 강의

이래저래, 공부를 너무 대충하는 것 같아 참조차 적어보기 위해 만든 블로깅

머신 러닝의 숲을 먼저 살펴보자면, 알고리즘까지 나열하자면 지금은 한도끝도 없이 많다.

다만, 어떤 식으로 분류가 되는지에 대해서는 원형 까지인데, 이정도는 알고있는것이 좋을 것 같다.

먼저 정통적인 방식은 Supervised Learning인데,

지도학습은 레이블이 있는 상태에서 학습하는 방식으로써, 학습데이터로 주어진 데이터의 피처와 레이블값을 머신러닝 알고리즘으로 학습, 모델을 생성하고, 이 모델에 피쳐를 줬을 때의 레이블 값을 예측하는 것이다.

여기에는 분류와 회귀가 있다.

분류는 결정트리, KNN, SVM, Navie Bayes, Neural net등의 다양한 알고리즘이 있으며 Ensemble이란 알고리즘을 결합하여 예측을 수행하는 방식으로 베깅, 부스팅, 볼팅 등이 있다.

Random forest 경우도 결정트리를 부스팅한 것으로써, Xgboost, LightGBM 또한 결정트리의 일종이라고도 볼 수 있다.

https://www.robotstory.co.kr/raspberry/?board_name=raspberry_bbs&mode=list&search_field=fn_user_pid&search_text=426&board_page=2&list_type=list&lang=ko_KR

결정트리

결정트리는 이해하기 쉬운 알고리즘으로써, 데이터에 있는 규칙을 학습으로 찾아내 트리 기반의 분류 규칙을 만드는 것이다. 단순하게 말하면 분기문을 만들어 구분한다고 생각하면 되겠다.

결정 트리의 경우 루트노드, 규칙이 있는 서브노드와 결정된 값이 들어있는 리프노드가 있다. 그리고 새로운 규칙이 추가될때 이에 기반한 서브트리가 생성된다.

이때, 많은 규칙이 있다는 것은 분류를 결정하는 방식이 복잡하다는 것이고, 이는 과적합, 성능저하의 원인이 된다.

결정트리의 핵심 아이디어는 불순도를 낮추는 것에 있다. 불순도란 정보의 복잡도(얼마나 균일한가)를 의미하며, 불순도를 수치화한 값에는 지니계수(Gini coefficient)와 엔트로피(Entropy)가 사용된다.

아무래도, 동일한 데이터에서도 결정트리는 여러 개가 나올 수가 있는데, 여기서 불순도를 이용해 더 효과적인 결정트리를 결정할 수 있다.

subNode에서 데이터가 분리되었을 때, 더 순도가 높은 데이터가 많이 나오게 되는 속성이 더 효과적이라고 할 수 있으며, 이때 순도가 높다는 것은 분류된 레이블 값이 동일한 것, 즉, 레이블 값이 다 같은 것을 말한다.

이때, 분류가 완료된 리프노드의 엔트로피는 0이다.

Decision Tree의 성능측정은 entropy(T)를 통해 이뤄지며 entropy(T)= -p₊log(p₊) -p_-log(p_-)이다.

이때, p₊, p_-는 각각 positive position(순도가 pure한 것/전체), nagative position(순도가 pure하지 않은 것/전체)를 말한다.

예를 들어 10개 데이터의 클레스를 분류한 결과, 7개는 예측이 잘 되지만 3개는 안된다면

p₊, p_-는 각각 [7+, 3-]이고, entropy(T)= -(7/10)log(7/10)-(3/10)log(3/10)=0.881 이다. (entropy 는 0to1 이다)

조금 더 살펴보자면, 결정트리 알고리즘에는 ID3, CART가 있는데, 이때 ID3은 엔트로피를 사용하고, CART는 지니계수를 사용한다. (이 내용 공부후 추가할 것)

랜덤 포레스트

랜덤 포레스트란 배깅을 사용하는 앙상블으로써, 배깅은 같은 알고리즘으로 여러 개의 모델을 만들어서 보팅으로 최종 결정하는 알고리즘이다.

기본적인 개념은 여러 개의 결정트리 모델이 전체 데이터를 샘플링해 개별적으로 학습을 수행 한 뒤, 모든 분류기가 보팅을 통해 예측 결정을 하는 방식이다.

이때, 보팅이란 여러개의 모델이 학습하고 예측한 결과를 보팅으로 최종 예측하는 것으로써, 하드보팅과 소프트 보팅이 있다.

하드 보팅은 일종의 다수결 원칙으로, 다수의 모델이 결정한 예측값을 최종 보팅값으로 선정하는 것이고, 소프트 보팅은 모델의 레이블 값 결정 확률을 모두 더하고 이를 평균해서 이 중 가장 확률이 높은 레이블 값을 최종 보팅 결과값으로 선정하는 것으로써, 일반적으로 소프트 보팅이 사용된다.

랜덤 포레스트의 모델별 알고리즘은 결정트리이지만, 각각의 모델이 학습하는 데이터는 전체 데이터에서 일부가 중첩되도록 샘플링된 데이터셋이다. 이렇게 여러 개의 데이터셋을 중첩되게 분리하는 것을 부트스트레핑(bootstrapping)분할 방식이라고 하며, 

이렇게 부트스트레핑으로 분할된 데이터셋에 결정트리 모델을 각각 적용하는 것이 랜텀 포레스트이다.

GBM

다음으로 GBM을 살펴보면

부스팅 알고리즘이란 여러 개의 약한 학습기를 순차적으로 학습-예측하며 잘못 예측된 데이터에 가중치를 부여하여 오류를 개선하며 학습하는 것이다.

대표적으로 AdaBoost와 GradientBoost가 있다. 

KNN

KNN을 먼저 설명하자면 이건 매우 쉽다.

간단하게 가장 가까운 점 몇개를 가지고 분류하겠다는 문제.

예측하고 싶은 data에서 가장 가까운 k개의 이웃을 구하고, 거리를 measure하고, 그들의 class값을 체크한 뒤 조정해서 예측하는 것이다.

다음이 SVM인데, 이는 기본적으로 그룹을 분리하기 위해, 데이터들과 가장 거리가 먼 초평면을 선택하여 분리하는 방법을 말한다.

기본적인 아이디어는 어떻게 공간을 나눌 것인가에서 출발하며, 

다음 블로그를 참조했다. 

https://ratsgo.github.io/machine%20learning/2017/05/30/SVM3/

https://velog.io/@shlee0125/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EC%A0%95%EB%A6%AC-Support-Vector-Machine-05.-Why-does-SVM-maximize-margin

https://www.slideshare.net/freepsw/svm-77055058

https://jaejunyoo.blogspot.com/2018/01/support-vector-machine-1.html#mjx-eqn-eqdr

https://sanghyu.tistory.com/7?category=1122189

먼저 SVM을 설명하기 전에, 선형분류에 대해 얘기를 하는 것이 이해에 도움이 될 것 같다.

간단히 두개의 클레스를 분류하는 문제를 생각해보면, 

위와 같은 데이터가 주어졌을 때, 이를 분류하기 위한 선을 하나 그어보자면

아래와 같은 모양이 될 것이다.

이고, $$y=w_{1}x_{1}+b$$꼴의 식이 만들어 질 것이고, 이때, $$y=-x+6$$이라면, 위의 선중 실선이 될 것이다.

여기서 식을 조금 다르게 바라보자

가로축, 세로축이 각각 $$x_{1},x_{2}$$ 라고  한다면, $$y=w_{1}x_{1}+w_{2}x_{2}+b$$꼴이 될 것이고, 각각을 

선형 분류는 가장 적절한 경계선이 되도록 w와 b를 결정하는 것이다.

이 적절함은 손실함수로 찾을 수 있다.

여기서 발전한 형태가 피셔의 판별분석이라 할 수 있다.

위의 그림에서 왼쪽 그림이 오른쪽 그림보다 평균간의 거리는 더 멀지만, 경계선은 오른 쪽이더 적합해 보인다.

원인은 왼쪽은 클래스의 y값이 넓지만, 오른쪽은 좁게 모여있기 때문으로, 선형판별분석은 클래스간의 차이는 크게, 클래스 내의 차이는 작게 만드는 w를 가장 좋은 w로 본다.

정리하면 아래의 식에서 J를 최대화하는 w를 찾는 것이다.

$$J=\frac{(m_{1}-m_{2})^{2}}{s_{1}^{2}+s_{2}^{2}}$$

$$m_{i}:i번째 클래스의 평균, s_{i}:i번째 클래스의 표준편차$$

이런 아이디어가 선형분류라고 한다면,

SVM은 클래스를 나누는 선과 가장 가까운 점의 거리를 최대화하는 것이 아이디어다.

선형 판별을 할 때, 클래스를 나누는 선은 여러 개가 나올 수 있는데, 이중 어떤 것을 선택할 것인지에 이 아이디어가 쓰이는데, 

위의 그림에서 아래 그림이 SVM에 대해 잘 설명하고 있다. 선에서 가장 가까운 점이 Support Vectors이고, Margin이 선과 SupportVectors와의 거리를 말한다.

이 마진을 결정하는 각 클래스의 샘플이 서포트 벡터이며, 새로운 데이터가 들어왔을 때 클래스를 구분하는 기준이 된다.

이 거리가 멀수록 신뢰도가 올라가게 되고 이 거리를 최대화하는 것을 하드마진이라 한다.

다만 이 SVM의 단점이라 한다면, 실제 데이터에서 노이즈나 이상치에 대처가 어렵다는 것이다.

그래서 소프트 마진이라는 것이 생기게 되었는데,  

 위와 같은 그림이 현실에 가까운 데이터라 할 수 있으며, 하드마진은 이에 대응하기가 어렵다.

또한 위의 사진과 같이 선형 분류가 되지 않는 경우는...... 사실상 성능을 낼수가 없다.

따라서, 마진에 잉여(slack)를 허가해 줌으로써 개선한 것이 소프트 마진 svm이다.

훈련 데이터에 이상치나 노이즈가 있다는 점에 무게를 두고, 결정경계의 근방에서 발생할 노이즈, 이상치는 좀 틀려도 되도록 여유를 주고 넓은 마진을 가지게 하는 것이다.

각 훈련 데이터 샘플 $$(x_{i},y_{i})$$마다 잉여 변수를 대응시켜, 샘흘이 마진의 폭 안으로 $$ξ_{i}$$만큼 파고드는 것을 용인해주는 것이다.

-커널트릭

eigen vector을 잘 설명해주는 그림이 있어 위키피디아에서 가져왔다.

SVM

Naive Bayes

다음으로 Naive Bayes Learning을 살펴보면, 

기본적 아이디어는 조건부 확률을 말하는 것으로 예를 들어 2개의 random x,y가 있을 때 x의 조건하에 y일 확률을 말한다.

즉 어떤 x가 주어졌을 때 어떤 클래스에 속할 확률을 구해서 그중 가장 큰 확률을 주는 x가 y라고 보겠다는 것이다.

예를 들자면, 

위와 같은 표가 주어진다고 하자.

8번째에서 내가 골프를 칠 것인가를 결정하자면\[\sum_{n=1}^{100} {n}\]

골프를 칠 것인가가 Yes일 떄의 확률은 $$\frac{sunny}{Y일때}\frac{mild}{Y일때}\frac{high}{Y일때}\frac{\frac{Y}{전체}}{P(i_{8})}=\frac{1}{4}\frac{1}{4}\frac{2}{4}\frac{\frac{4}{7}}{P(i_{8})}=\frac{1}{56P(i_{8})}$$ 이고,

골프를 칠 것인가가 No일 떄의 확률은 

$$\frac{sunny}{N일때}\frac{mild}{N일때}\frac{high}{N일때}\frac{\frac{N}{전체}}{P(i_{8})}=\frac{2}{3}\frac{1}{3}\frac{2}{3}\frac{\frac{3}{7}}{P(i_{8})}=\frac{4}{63P(i_{8})}$$

이 나온다.

이때, N일 때가 더 크므로 골프를 치는가의 여부는 N으로 결정된다.

APC의 BE700-kr의 정품 배터리 RBC-17의 경우

라벨을 떼어보면 다양한 제조사에서 납품함을 알 수 있다.

wp9-12shr (출처:https://www.bonobono.com/2022/07/21/apc-be700-kr-ups-battery/)
hr1234w (출처: https://comterman.tistory.com/2065)
cp1290 (출처: 직접 사용중인 것에서 확인)

특히 cp 1290의 경우->es 9-12 와 매우 동일한 datasheet를 가짐을 확인했다.(https://www.vision-batt.com/site/product_files/CP1290.pdf)

일단 내가 사용하며 오래 사용한 배터리가 cp1290의 라벨을 가지고 있음을 확인했고,

es-9-12의 데이터 sheet(https://almazroui-me.com/wp-content/uploads/2018/12/Rocket-Battery-ES-9-12-12V-9Ah-AGM-VRLA.pdf)를 확인해본 결과 설계수명이 더 길다는 점 외에 특이사항을 발견하지 못하였으므로

로케트 전지의 es9-12를 사용해볼 예정

Primary Reference:

Social Media Mining Reza Zafarani, Mohammad-Ali Abbasi, Huan Liu, Cambridge University Press 2014,http://socialmediamining.info

OVER VIEW

소셜 미디어는 인터넷 플랫폼을 이용해, 정보 및 경험을 보다 효율적으로 다른 사람들과 공유하고 토론하는 것을 명칭한다.

소셜 미디어의 주요 특성은 다음과 같다:

1. Participation- 소셜 미디어는 많은 사람의 기여와 피드백을 장려함으로, 미디어와 관객의 경계를 모호하게 만든다.

2. Openness- 대부분의 소셜 미디어 서비스는 피드백과 참여에 열려있으며, 투표, 의견 및 정보공유를 장려한다.

3. Conversation- 전통적 미디어는 일방적 소통이지만 소셜 미디어는 양방향 소통이다

4. Community - 소셜 미디어는 같은 관심사를 공유한 사람들간 커뮤니티가 빠르게 형성되고 소통이 가능하다

5. Connectedness - 대부분의 소셜 미디어는 링크를 사용한 연결성을 기반한다.

소셜 미디어 마이닝의 Challenges:

1. Big Data Paradox

- 소셜 미디어 데이터는 매우 방대하지만, 편향적인 특성이 있다. (어떤 사람은 친구가 1000명이고 어떤 사람은 10명.. )

- 개인의 입장에서는 연결된(가용할 수 있는) data가 적다. 

2. Obtaining Sufficient Samples

- 충분한 샘플을 얻기가 힘들다. (특정 샘을이 전체 데이터를 대표한다고 볼 수 있는가..)

3. Noise Removal Fallacy

- 노이즈를 너무 많이 제거하면 데이터가 sparse해진다.

- 노이즈의 정의가 상대적이고 복잡하며 작업에 따라 다르다(어떤 주제에서의 노이즈도 다른 주제에서는 노이즈가 아닐수 있음)

4. Evaluation Dilemms

- 정답이 없기때문에, 평가가 어렵다. 근거가 없으면 어떻게 평가를 할수 있는가?

#2_SMM_Graph Essentials

Bridges of konigsberg 문제는, 두개의 섬과 강의로 나뉜 대륙이 7개의 다리로 연결 되어 있을때, 다리를 한번씩만 건너서 모든 곳을 방문할 수 있는가의 문제이다.

이 문제를 해결하는 방법은 그래프 표현을 이용하는 것으로, 오일러는 걷기의 시작, 끝을 제외하고 다른 모든 노드에 들어가고 나와야 하므로 이러한 노드에는 짝수개의 다리가 연결되어야 함을 증명했다.

네트워크는 그래프로 표현할 수 있고, (node -> route, connection->연결망) 네트워크 문제는 일반적으로 그래프 이론으로 나타낼 수 있다.

인터넷의 시각화

소셜 네트워크 분석은 사회과학, 통계, 그래프 이론, 복잡한 네트워크, 컴퓨터 과학의 연합 분야라고 할 수 있다.

- 그래프의 기초

 네트워크는 그래프 또는 선으로 연결된 점의 집합이라 할 수 있다. 

점은 node, actor, vertices, vertex 등으로 볼수 있고

연결은 edges, ties라고 볼 수 있다.

그래프의 노드 V는  V={v_1, v_2, ..., v_n}로 나타내고, size of the graph |V|=n

Edge는 node간의 ties, relationships를 나타내며 다음과 같이 표현한다.

E = {e_1, e_2, ..., e_m}

Number is edgs( size of the edge-set):|E|=m

edge는 e(v1,v2)와 같이 표현하며, 방향성이 있는 경우와 없는 경우가 있다.

(a)의 경우 e(v2,v1)과 e(v1,v2)는 다르지만, 방향성이 없는 (b)에서는 동일한 표현이다.

어떤 노드 V가 있을 때 연결된 노드를 neighborhood라 하고, N(v)라고 표현한다.

(b)에서 N(v7)={v1, v4, v6}

방향성이 있는 그레프의 경우 in, out가 존재하므로 Nin(v), Nout(v)로 표현한다.

Degree(차수)와 차수 분포

- 방향성이 없는 그래프에서 degree의 합은 edge수의 2배이다.

\sum(d_i)=2|E|

- degree의 합은 짝수이다.

- 모든 방향성있는 그래프에서 in-degrees의 합은 out-degrees의 합과 같다. 

집에 개인적으로 nas를 운용중이였는데 이게 슬슬 수명이 다되어가는거같기도 하고,,

자작이라 너무 조악한 상황이었기에 새로 nas를 제작하려고 메인보드를 알아보던중 

j4105라는 모델이 2월에 새로 출시하는것을 알게되었고 해당모델을 주문했다.

용도는 nas이기에 쓸데없는기능 없는 j4105b로 주문하였고

최대한 공간활용을 원하기에 작으면서도 3.5가 들어가는 모델로 케이스도 주문했다.

사실 개인적으로 asrock를 신뢰하지는 않는다. 또한 사정상 크게 신경을 쓸수가 없기에 일단 구축후 방치할 수 있는

신뢰도가 높은 system을 구축하길 바랬고, 기가바이트 보드를 내심 마음에 두고 있었으나

그때까지 기다릴수가 없을것 같았고, 요즘 내구도향상과 3년무상as라는 말을 믿고 일단 asrock모델을 출시직후 샀다.

케이스의경우 g3이라는 모델을 이용했는데 해당제품의 경우 dc to dc 120w가 내장되어있고, 아답타포함 6만원이다.

다만 알리직구 구매시 케이스는 45000가량인데 36000정도에 구매가 가능하고 아답타의경우 내가 산 72W는 만오천원선에 구매 가능하다

만원차이에 빠른 배송과의 시름이라 할 수 있겠다.

나는 그냥 국내주문했다.

메인보드다 신난다 신나 오랜만에 보는 itx보드

사실 팬리스라서 발열걱정을 많이 했는데 생각보다 심하지는 않았다.

gui 바이오스를 지원한다.

거기다 요즘 메인보드는 바이오스에서 인터넷연결과 업데이트를 지원한다(!!) 거의 운영체제급인걸.;;;

펜을 달았을때 팬속도 1-255사이의 숫자로 조절가능하며 꽤나 샛팅이 디테일하다.

뭤보다 마우스가 사용가능한 gui라는건 점점 아저씨가 되어가는 내게 꽤나 메리트가 크다

그런데 조립하다보니 꽤나 큰 문제에 봉착했다.

대충 안쓰는 하드를 시험용으로 끼워보니 이게 2.5최적화 케이스인지 팬리스 cpu쿨러와 거의 닿다시피한다.

nas용하드는 고용량이라 아예 둘이 닿아있을거같은데... 50도만 넘어가도 하드는 사망이 임박이라 봐야하고..

하...머리가 아파온다...

그렇게 고민고민하다가 결국 결정했다.

안되면 만들지 뭐 ^^

안쓰는 2베이 하드 케이스가 본가에 있던걸 기억해내고 가져왔다.

그리고 무기고로 직행.

알맞은 무기를 고른다.

정밀작업에 적당한건 역시 그라인더(!?)지

가운대에 맞추면 이쁘겠지만 나중에 공간활용이나 추가를 위해 가장자리에 케이스 아래 홀과 맞추어 잘라줬다.

알루미늄이 아주 두꺼운게 든든하다.

그리고 sata케이블과 하드 전원이 들어가기 위한 구멍도 슬적 뚫어주고...

드릴링뒤 부라인더 리벳을 박고

리벳건으로 리베팅해주면 아주 견고하게 흔들림없이 고정된다 . (사실 파는 케이스도 전부 리벳으로 고정된다. 리벳 하나있음 짱편함)

그리고 다시 조립한 모습

후면

측면

사실 이런 조악한걸 만들기 싫어서 기성품을 사는건데 하드베이 머가리가 어디론가 사라져서 포맥스 잘라다가 만들어서 끼웠다 ㅠㅠ

뒷면의경우 손으로 하드를 뺴고 넣을수 있도록 rgb케이블의 나사를 뺴서 잠그고

공기청청기용 먼지필터를 근처에서 주워다가 대충 달아줬다. 그리고 사진상엔 안보이지만

상단부에 50mm팬 두개, 하드베이에 50mm 팬 배기를 달아서

각각 cpu, board 3pin fan 단자에 물려주었다.

기존에 쓰던 노트북 보드와 각종 어댑터로 자작한 nas와 비교샷이다.

훨씬 깔끔하네그려.

심지어 이번 나스는 정전후 자동재부팅기능도 있다지 오홍홍

열어보니 역시 먼지투성이에 죽어가고있다. 2010년산 su7300cpu 기반의 노트북을 개조한 nas였다.

사실 혼자쓰기엔 성능 차고 넘쳤고, 2010년기준 듀얼코어에 tdp10w 였으며, 노트북보드기반이기에 3.5하드의경우 별도로 12v만 공급해줘야했다.

네트워크 칩셋도 퀼컴 아데로스였고, 보드도 에이수스기반이였으니 사실 지금 그대로도 2년정도는 더 버텨줄것 같긴하다.

그래서 일단 안정성테스트동안은 본가에 두기로 한다.

그리고 이놈은 셋방살이 시작.

일단 j4105기반으로 nas를 구성하시려는 분들을 위해 조언을 하자면 

제 보드는 j4105b-itx이며 xp놀로지 구성시 916p 기반의경우 설치까지는 잘 됩니다만 랜 드라이버가 심기는 과정에서 사라지는것 같습니다.

여러번 복구나 재설치를 해봐도 916버전은 사용할 수 없었으며

jun's mod 자체는 매우 잘 동작합니다. (오히려 퀼컴이 동작하지 않습니다.... jun님이 주머니사정 가벼우신 분들을 위해 신경쓰신것 같습니다.)

다만 공유기가 브로드컴 기반이고 보드렌이 리얼택이여서인지 네트워크속도가 가끔식 미분불가한 그래프를 그리기는 합니다.

2일간 모니터링결과 아직까지는 안정적이라는 평가를 주고싶습니다.

보드에 무선랜 단자가 있는걸 보니 보드pcb는 재활용인것같긴 하지만 보드의 안정성 자체는 나쁘지 않은 수준이라고 보여집니다.

다만 j4105의 경우 ddr4f를 기반하기때문에 초기비용이 꽤나 들어가실것으로 보여집니다.

발열자체는 꼭 기가바이트를 쓰지 않아도 풀로드시에도 50도를 넘나듭니다.

하드의경우 팬의 영향인지 30도를 넘지 않더군요

이후의 확장까지 생각하면 제작케이스에 매우 보람을 느낍니다. (공기 배기, 순환구조도 매우 만족이거든요 ㅎㅎ)

+이후에는 안쓰는 led모니터패널 재활용편을 올려보도록 하겠습니다.