Intreoduction
Bayesian Decision Theory
- 근본적인 통계 패턴 분류 문제에 대한 접근
- 다양한 분류간의 트레이드 오프를 정량화하는 것을 기반
- 확률을 이용한 결정과 그러한 결정에 수반되는 비용
State of nature ω 자연의 상태
- $\omega=\omega_1$ 을 위한 sea bass, $\omega=\omega_2$ 를 위한 salmon
- 자연의 상태는 예측불가
- 확률적으로 기술되어야 하는 변수
A priori probability
- Seabass, salmon에 대한 사전지식의 반영
$P\left(\omega_1\right):$ Seabass일 사전확률
$P\left(\omega_2\right):$ Salmon일 사전확률
$P\left(\omega_1\right)+P\left(\omega_2\right)=1$ (단, 다른 생선이 없다면.)
Decision Rule
- 물고기를 보지 못하고 결정해야 한다면?
$P\left(\omega_1\right)>P\left(\omega_2\right)$ 면 $\omega_1$로 판정, 반대라면 반대로 판정
클레스-조건부(class-conditional)확률 밀도 함수 $p(x \mid \omega)$
- 자연의 상태가 ω 라고 주어졌을 때, x 에 대한 확률 밀도 함수
$p\left(x \mid \omega_1\right), p\left(x \mid \omega_2\right)$간의 차이는 Seabass와 Salmon의 모집단 간 밝기의 차이를 묘사

부류 $\omega_j$ 에 있고 특징 값x 를 갖는 패턴을 발견할 결합 확률 밀도는 두 가지 방법을 쓸 수 있다:
$p\left(\omega_j, x\right)=P\left(\omega_j \mid x\right) p(x)=p\left(x \mid \omega_j\right) P\left(\omega_j\right)$
Bayes formula
$P\left(\omega_j \mid x\right)=\frac{p\left(x \mid \omega_j\right) P\left(\omega_j\right)}{p(x)}$
이때 이 두부류의 경우는 $p(x)=\sum_{j=1}^2 p\left(x \mid \omega_j\right) P\left(\omega_j\right)$. posterior $=\frac{\text { likelihood } \times \text { prior }}{\text { evidence }}$
Bayes 공식은$x$ 의 값을 관찰함으로써 사전확률prior을 사후확률posterior(특징$x$ 가 측정되었을 때 자연 상태가$\omega_j$ 일 확률) 로 전환할 수 있다. $p\left(x \mid \omega_j\right)$는 $x$에 대한 $\omega_j$의 우도(likelihood)라고 부른다.

$P\left(\omega_1\right)=\frac{2}{3}$ and $P\left(\omega_2\right)=\frac{1}{3}$
Probability of error when decision is made
결정 방법은 $P($ error $\mid x)=\left\{\begin{array}{l}P\left(\omega_1 \mid x\right) * \text { if decide } \omega_2 \\ P\left(\omega_2 \mid x\right) * \text { if decide } \omega_1\end{array}\right.$
- 결정을 내릴 때 오류가 나올 확률은,$P($ error $)=\int_{-\infty}^{\infty} p($ error,$x) d x=\int_{-\infty}^{\infty} P($ error $\mid x) p(x) d x$ 만일 모든 x에 대해 $P(\operatorname{error} \mid x)$ 를 작게 만든다면 이 적분은 가능한 작아야 한다.
$P\left(\omega_j \mid x\right)=\frac{p\left(x \mid \omega_j\right) P\left(\omega_j\right)}{p(x)}$
Bayes Decision Rule (for minimizing the probability of error)
- Decide $\omega_1$ if $p\left(\omega_1 \mid x\right) P\left(\omega_1\right)>p\left(\omega_2 \mid x\right) P\left(\omega_2\right) ; \omega_2$ 로 판정 otherwise
- $\boldsymbol{p}(\boldsymbol{x})$ : 는 결정에 있어서는 크게 중요하지 않음 $\left(P\left(\omega_1 \mid x\right)+P\left(\omega_2 \mid x\right)=1\right)$
Decide $\omega_1$ if $p\left(\omega_1 \mid x\right) P\left(\omega_1\right)>p\left(\omega_2 \mid x\right) P\left(\omega_2\right) ; \omega_2$ 로 판정 otherwise
사후 확률의 역할을 강조.
- 만일 어떤 x에 대해서 $p\left(x \mid \omega_1\right)=p\left(x \mid \omega_2\right)$라면 판정은 전적으로 사전 확률에 의해 정해진다.
- $P\left(\omega_1\right)=P\left(\omega_2\right)$라면 판정은 전적으로 우도$p\left(x \mid \omega_j\right)$에 근거하게 된다.
Bayesion decion theory – continuious features(연속적 특징)
Bayesian Theory의 일반화
- 둘 이상(more than one feature)의 특징을 사용하는 것을 허용하는 것
- 스칼라 x
를 특징vector x
로 대체
- x
는 특징공간이라고 부르는 d
-차원 유클리드 공간 Rd
에 속함
Bayesion decion theory – continuious features(연속적 특징)
Bayesian Theory의 일반화
- 둘 이상(more than one feature)의 특징을 사용하는 것을 허용하는 것
- 스칼라 x 를 특징vector x 로 대체
- x 는 특징공간이라고 부르는 d-차원 유클리드 공간 $\mathbb{R}^d$ 에 속함
- 셋 이상(more than two states)의 자연의 상태를 허용하는 경우
- $\left\{\omega_1, \ldots, \omega_c\right\}: c$개의 자연의 상태(“categories”)의 유한 집합
- 분류 외의 행동을 허용하는 것
- $\left\{\alpha_1, \ldots, \alpha_a\right\}$: a개의 가능한 행동의 유한 집합
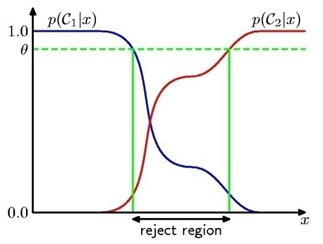
- 오류 확률(probability of error)보다 더 일반적이라 할 수 있는 손실 함수(loss function)를 도입.
- 손실 함수는 각 행동의 비용을 정확하게 나타내며, 확률 측정을 판정으로 전환에 사용된다.
$\lambda\left(\alpha_i \mid \omega_j\right)$ : 자연의 상태가 $\alpha_i$ 일 때, $\omega_j$ 라는 행동을 취해서 초래되는 손실
$P\left(\omega_j \mid x\right)=\frac{p\left(x \mid \omega_j\right) P\left(\omega_j\right)}{{p(x)}}$ 이때, $\quad p(x)=\sum_{j=1}^c p\left(x \mid \omega_j\right) P\left(\omega_j\right)$
행동 $\alpha_i$를 취하는 것과 관련된 기대 손실은 단순하게 $R\left(\alpha_i \mid x\right)=\sum_{j=1}^c \lambda\left(\alpha_i \mid \omega_j\right) P\left(\omega_j \mid x\right)$
- 판정-이론 용어로는 기대 손실을 리스크라고 부르며, $R\left(\alpha_i \mid x\right)$ 를 조건부 리스크라고 부른다.
- 문제는 $P\left(\omega_j\right)$에 대해 전체적 리스크를 최소화하는 판정 룰을 찾는 것.
$R=\int R(\alpha(x) \mid x) p(x) d x \quad R$ : 최소화된 전체적 리스크
- 전체적 리스크를 최소화하기 위한 조건부 리스크 계산 $R\left(\alpha_i(x)\right)$ 가 가능한 작도록 $\alpha(x)$가 선택된다면 전체적 리스크는 최소화
$R\left(\alpha_i \mid x\right)=\sum_{j=1}^c \lambda\left(\alpha_i \mid \omega_j\right)\left(\omega_j \mid x\right)$
$i=1, \ldots, a$ 에 대해 계산하고, $R\left(\alpha_i \mid x\right)$ 가 최소인 행동 $\alpha_i$ 를 선택
Bayesion decion theory – 두 부류(Two-Category) 분류
- $\alpha_1$: 자연의 참 상태가 $\omega_1$ 이라고 판정을 내리는 것
- $\alpha_2$: 자연의 참 상태가 $\omega_2$ 이라고 판정을 내리는 것
- $\lambda_{i j}=\lambda\left(\alpha_i \mid \omega_j\right)$: 자연의 참 상태가 $\omega_j$일 때 $\omega_i$라고 판정시 따르는 손실 이를 적용해서 $R\left(\alpha_i \mid x\right)=\sum_{j=1}^c \lambda\left(\alpha_i \mid \omega_j\right)\left(\omega_j \mid x\right)$ 를 다시 쓰면
- 조건부 리스크 $$
\begin{aligned}
& R\left(\alpha_1 \mid x\right)=\lambda_{11} P\left(\omega_1 \mid x\right)+\lambda_{12} P\left(\omega_2 \mid x\right) \\
& R\left(\alpha_2 \mid x\right)=\lambda_{21} P\left(\omega_1 \mid x\right)+\lambda_{22} P\left(\omega_2 \mid x\right)
\end{aligned}
$$
$\lambda_{11}, \lambda_{22}$ 는 잘한 것
- 최소 리스크 판정 룰을 표현하는 다양한 방법
1. $R\left(\alpha_1 \mid x\right)<R\left(\alpha_2 \mid x\right)$ 이면 $\omega_1$ 로 판정
2. $\left(\lambda_{21}-\lambda_{11}\right) P\left(\omega_1 \mid x\right)>\left(\lambda_{12}-\lambda_{22}\right) P\left(\omega_2 \mid x\right)$ 일 때 $\omega_1$ 이라고 판정(사후확률로 표현)
3. $\left(\lambda_{21}-\lambda_{11}\right) p\left(x \mid \omega_1\right) P\left(\omega_1\right)>\left(\lambda_{12}-\lambda_{22}\right) p\left(x \mid \omega_2\right) P\left(\omega_2\right)$ 이면 $\omega_1$ 로 판정하고 아니면 $\omega_2$ 로 판정 (Bayes공식을 사용함으로 사후 확률을 사전 확률과 조건부 밀도로 대체)
4. $\lambda_{21}>\lambda_{11}$ 이라는 논리적 가정 하에서 만약 $\frac{p\left(x \mid \omega_1\right)}{p\left(x \mid \omega_2\right)}>\frac{\lambda_{12}-\lambda_{22}}{\lambda_{21}-\lambda_{11}} \frac{P\left(\omega_2\right)}{P\left(\omega_1\right)}$ 이면 $\omega_1$ 로 판정
(Likelihood ratio: 이 형태의 판정 룰은 확률 밀도들의 $x$-종속성에 초점을 맞춘다. $p\left(x \mid \omega_j\right)$ 를 $\omega_j$ 의 함수(즉, 우도 함수)로 간주하고 우도 비 $\frac{p\left(x \mid \omega_1\right)}{p\left(x \mid \omega_2\right)}$ 를 만들 수 있다. 따라서 Bayes 판정 룰은 관찰 $x$ 에 독립적인 어떤 문턱 값을 우도비가 넘으면 $\omega_1$ 로 판정할 것을 요구하는 것으로 해석)
Bayesion decion theory – Minimum-error-rate Classification(최소 에러율 분류)
에러를 피하기 위해서는 자연의 상태와 차이가 가장 적은(오류를 최소화하는) 판정 룰을 찾는 것이 당연하다.
Zero-One loss function
$\lambda\left(\alpha_i \mid \omega_j\right)=\left\{\begin{array}{ll}0 & i=j \\ 1 & i \neq j\end{array} i, j=1, \ldots, c\right.$
- 옳은 판정에 대해서는 손실이 없음
- 모든 에러에 단위 손실을 부여
- 모든 에러는 같은 비용이 든다.
$\sum_{j=1}^c \lambda\left(\alpha_i \mid \omega_j\right) P\left(\omega_j \mid x\right)=\sum_{j \neq i} P\left(\omega_j \mid x\right)=1-P\left(\omega_i \mid x\right)$
조건부 리스크를 최소화하는 행동을 선택 if. $P\left(\omega_i \mid x\right)>P\left(\omega_j \mid x\right)$ we decide $\omega_i \forall j \neq i$
The likelihood ratio $p\left(x \mid \omega_1\right) / p\left(x \mid \omega_2\right)$
$\frac{p\left(x \mid \omega_1\right)}{p\left(x \mid \omega_2\right)}>\frac{\lambda_{12}-\lambda_{22}}{\lambda_{21}-\lambda_{11}} \frac{P\left(\omega_2\right)}{P\left(\omega_1\right)}$
Classifiers, Discriminant functions, and Decision surfaces
다분류 경우
패턴 분류기를 표현하는 다양한 방법중에 가장 쓸만한 방법중 하나
- 판별함수들$g_i(x), i=1, \ldots, c$ 에 의한 것
- 만일 $\boldsymbol{g}_{\boldsymbol{i}(\boldsymbol{x})}>\boldsymbol{g}_{\boldsymbol{j}}(\boldsymbol{x}) \forall \boldsymbol{j} \neq \boldsymbol{i}$ 이면 특징 벡터 $x$ 를 클레스 $\omega_i$ 에 할당한다.
분류기
- 분류기는 c개의 판별 함수를 계산하고 최대 판별식에 해당하는 부류를 선택하는 네트워크 또는 기계
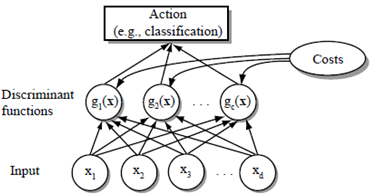
$g_i(x)=\left\{\begin{array}{c}g_1(x)=0.1 \\ g_2(x)=0.05 \\ \vdots \\ g_{n(x)}=0.85\end{array}\right.$ 중 가장 큰 것 선택
판별 함수들의 선택은 유일하지 않다.
$g_i(x)=-R\left(\alpha_i \mid x\right)$ (for risk)
$g_i(x)=P\left(\omega_i \mid x\right) \quad($ for minimum $-$ error $-$ rate $)$
판별함수의 수정이 가능
판정에 영향을 주지 않고 우리는 항상 모든 판별 함수들을 같은 양의 상수로 곱하거나 같은 상수를 더해서 이동시킬 수 있다. 더 일반적으로는 모든 $g_i(x)$ 를 단조증가함수 $f(\cdot)$ 에 의해 $f\left(g_i(x)\right)$ 로 대체시, 그로인한 분류는 변하지 않는다. 이것은 현저한 분석 및 계산 단순화로 이끌 수 있다.
$\left\{\begin{array}{l}g_i(x)=P\left(\omega_i \mid x\right)=\frac{p\left(x \mid \omega_i\right) P\left(\omega_i\right)}{\Sigma^c p\left(x \mid \omega_j\right)^{P\left(\omega_j\right)}} \\ g_i(x)=p\left(x \mid \omega_i\right) P\left(\omega_i\right) \\ g_i(x)=\ln p\left(x \mid \omega_i\right)+\ln P\left(\omega_i\right)\end{array}\right.$
모든 판정 룰의 효과는 특징 공간을 $c$ 개의 판정 영역 $\mathcal{R}_1, \ldots, \mathcal{R}_c$ 로 나누는 것
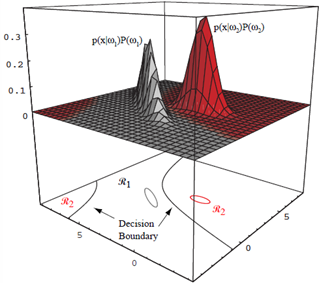
두 분류 경우
이분기(dichotomizer)
두 부류 경우는 다부류의 일종이나 정통적으로 독립해 다뤄왔다.
두 판별 함수 대신 단일 판별 함수를 정의하고 판정하는 것이 더 보편적이다.
$g(x) \equiv g_1(x)-g_2(x)$
$g(x)>0$ 이면 $\omega_1$, 아니면 $\omega_2$ 로 판정
$\boldsymbol{g}(\boldsymbol{x})=\boldsymbol{P}\left(\boldsymbol{\omega}_1 \mid \boldsymbol{x}\right)-\boldsymbol{P}\left(\boldsymbol{\omega}_2 \mid \boldsymbol{x}\right)$
$\boldsymbol{g}(\boldsymbol{x})=\ln \frac{\boldsymbol{p}\left(\boldsymbol{x} \mid \boldsymbol{\omega}_1\right)}{\boldsymbol{p}\left(\boldsymbol{x} \mid \boldsymbol{\omega}_2\right)}+\ln \frac{\boldsymbol{P}\left(\boldsymbol{\omega}_1\right)}{\boldsymbol{P}\left(\boldsymbol{\omega}_2\right)}$
The normal density
왜 Normal density인가?
- 분석의 용이함(해석학적으로 다루기 쉬움)으로, 다변량 normal밀도, 또는 Gaussian밀도는 많은 관심을 받았다.
- 중요한 상황에 적합한 모델. class $\omega_j$에 특징벡터 x가 단일 또는 프로토타입 벡터 $\mu_i$의 연속적 값을 가지고 랜덤하게 오염된 버전일 경우에 적합.
Expectation (expected value)
$$
E[f(x)]=\int_{-\infty}^{\infty} f(x) p(x) d x
$$
만약 특징 $\mathrm{x}$ 의 값들이 이산 집합 $\mathrm{D}$ 의 점이라면.
$$
E[f(x)]=\sum_{x \in D} f(x) P(x)
$$
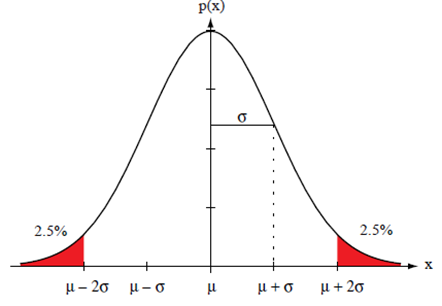
The normal density – 단변량 밀도
$p(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left[-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2\right]$
- 평균
$$
\mu=E[x]=\int_{-\infty}^{\infty} x p(x) d x
$$
- 분산
$$
\begin{aligned}
& \sigma^2=E\left[(x-\mu)^2\right]=\int_{-\infty}^{\infty}(x-\mu)^2 p(x) d x \\
& -\quad \boldsymbol{p}(\boldsymbol{x}) \sim \boldsymbol{N}\left(\boldsymbol{\mu}, \boldsymbol{\sigma}^2\right)
\end{aligned}
$$
$x$ 는 평균 $\mu$ 와 분산 $\sigma^2$ 에 의해 분포된다.
The normal density – 다변량 분포
$$
p(\boldsymbol{x}) \sim N(\boldsymbol{\mu}, \boldsymbol{\Sigma}) \quad p(\boldsymbol{x})=\frac{1}{(2 \pi)^{d / 2}|\boldsymbol{\Sigma}|^{1 / 2}} \exp \left[-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^t \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right]
$$
- 평균 벡터
$$
\text { - } \boldsymbol{\mu}=E[\boldsymbol{x}]=\int_{-\infty}^{\infty} \boldsymbol{x p}(x) d \boldsymbol{x}
$$
- 공분산 행렬 (Convariance)
$$
\Sigma=E\left[(\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^t\right]=\int_{-\infty}^{\infty}(\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^t p(x) d x{ }^*[x-\mu]=\left[\begin{array}{lll}
\sigma_{11} & & \\
& \ddots & \\
& \sigma_{n n}
\end{array}\right]
$$
- 통계적 독립성(statistical independence)
만약 $x_i$ 와 $x_j$ 가 통계적으로 독립적이면, $\sigma_{i j}=0$ 일 것이다. 만약 모든 비대각선 요소들이 0 이면, $p(x)$ 는 $x$ 의 요소들에 대한 단변량 노멀 밀도들의 곱으로 축소된다.
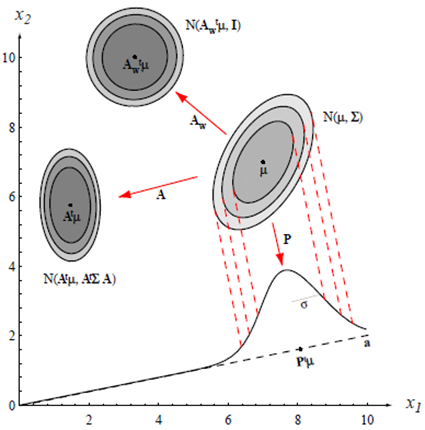
- 독립적이거나 아니거나, 결합적으로(jointly) 노멀하게 분포 하는 랜덤 변수들의 선형 결합(combination)은 노멀하게 분포한다.
$$
\begin{aligned}
& p(\boldsymbol{x}) \sim N(\boldsymbol{\mu}, \mathbf{\Sigma}) \\
& \boldsymbol{y}=\boldsymbol{A}^t \boldsymbol{x} \rightarrow p(\boldsymbol{y}) \sim N\left(\boldsymbol{A}^{\boldsymbol{t}} \boldsymbol{\mu}, \boldsymbol{A}^{\boldsymbol{t}} \boldsymbol{\Sigma} \boldsymbol{A}\right) \\
& * y=A^t y=\left[\begin{array}{lll}
y_1 \\
y_2
\end{array}\right]=\left[\begin{array}{ccc}
1 & \cdots & 0 \\
\vdots & A & \vdots \\
0 & \cdots & 1
\end{array}\right]\left[\begin{array}{l}
x_1 \\
x_2
\end{array}\right]
\end{aligned}
$$
-임의의 다변량 분포를 구형(spherical)분포로 변환(공분산 행렬이 항등 행렬 $I$ 에 비례하는 분포)할 수 있다. (백색변환)
$$
A_\omega=\Phi \Lambda^{1 / 2}
$$
$\boldsymbol{\Phi}$ : 열들이 $\Sigma$ 인 정규직교 고유 벡터들인 행렬
$\mathbf{\Lambda}$ : 해당 고윳값들의 대각선 행렬
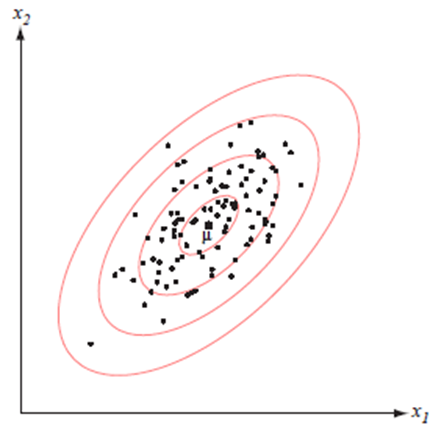
- 다변량 정규분포는 $\boldsymbol{d}+\boldsymbol{d}(\boldsymbol{d}+\mathbf{1}) / \mathbf{2}$ 개의 파라미터 즉, 평균 벡터 $\boldsymbol{\mu}$ 의 요소들과 공분산 행렬 $\boldsymbol{\Sigma}$ 에 의해 완전하게 정의된다.
- 아래 그림에서:↓
- 클러스터의 중심은 평균 벡터에 의해 결정
- 클러스터의 모양은 공분산 행렬에 의해 결정.
- 상수 밀도의 점들의 위치는 $(\boldsymbol{x}-\boldsymbol{\mu})^t \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})$ 가 상수 인 초타원체들이다
- 이 초타원체들의 주축은 $\Phi$ 에 의해 묘사되는 $\boldsymbol{\Sigma}$ 의 고유 벡터들에 의해 주어지며,
고윳값들 $(\boldsymbol{\Lambda})$ 은 이 축들의 길이를 결정한다.
- Mahalanobis distance (from $x$ to $\boldsymbol{\mu}$ ) 마할라노비스 거리 $r^2=(\boldsymbol{x}-\boldsymbol{\mu})^t \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})
(분산이 커지면, 거리는 작게 해석)
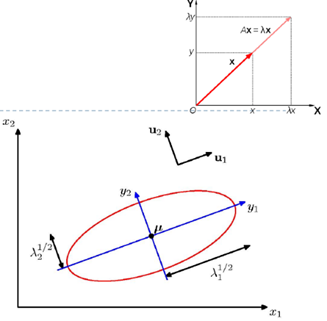
(PRML 2.3) The Gaussian Distribution
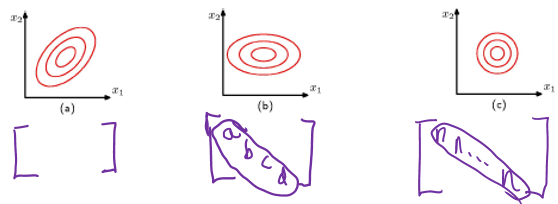
빨간색 선은 이차원 공간 $x=\left(x_1, x_2\right)$ 상에서의 상수 가우시안 확률 분포의 타원형 표면을 나타낸다. 여기서 말도는 $x=\mu$ 일 경우의 값의 $\exp (-1 / 2)$ 에 해당한다. 타원의 축들은 공분산 행렬의 고유 벡터들 $u_i$ 에 의해 정의 되 며, 각각의 축은 각각의 고윳값 $\lambda_i$ 에 대응된다.
이차원 가우시안 분포에서의 상수확률 밀도의 경로.
(a)는 공분산 행렬의 형태가 일반적일 경우
(b)는 공분산 행렬이 대각 행렬인 형태
(c)는 공분산행렬이 항등행렬의 상수배일 경우이며 이 경우 경로가 동심원의 형태를 띈다.
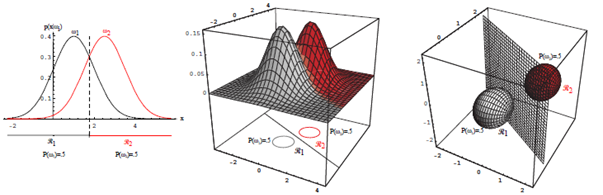
정규분포에 대한 판별 함수
- 최소 에러율 분류는 아래의 판별 함수로 달성될 수 있다.
$\begin{aligned} & p(\boldsymbol{x})= \frac{1}{(2 \pi)^{d / 2}|\boldsymbol{\Sigma}|^{1 / 2}} \exp \left[-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^t \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right] \text { 에 의해 } \\ & g_i(\boldsymbol{x})=-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)^t \boldsymbol{\Sigma}_i^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)-\frac{d}{2} \ln 2 \pi-\frac{1}{2} \ln \left|\boldsymbol{\Sigma}_i\right|+\ln P\left(\omega_i\right)\end{aligned}$
- 판별함수의 3가지 경우
1. $\boldsymbol{\Sigma}_i=\sigma^2 \mathbf{I}$
2. $\boldsymbol{\Sigma}_i=\boldsymbol{\Sigma}$
3. $\mathbf{\Sigma}_i=$ arbitrary
Case 1: $\Sigma_i=\sigma^2 I$
- 가장 간단한 경우
- 특징들이 통계적으로 독집적이고 각 특징이 같은 분산 $\sigma^2$를 가짐.
- 기하학적으로 샘플들이 같은 크기의 초구 클러스터에 놓이는 상황
- $i$ 번째 클래스에 대한 클러스터는 평균 벡터 $\mu_i$ 가 중심으로 함.
- $\Sigma_{\mathrm{i}}$ 의 행렬식과 역의 계산이 쉬움
$$
\left|\boldsymbol{\Sigma}_i\right|=\sigma^{2 d} \quad \boldsymbol{\Sigma}_i^{-1}=\frac{1}{\sigma^2} \mathbf{I}
$$
- $g_i(x)=-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)^t \boldsymbol{\Sigma}_i^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)-\frac{d}{2} \ln 2 \pi-\frac{1}{2} \ln \left|\boldsymbol{\Sigma}_i\right|+\ln P\left(\omega_i\right)$
$\boldsymbol{\Sigma}_i^{-1},\left|\boldsymbol{\Sigma}_i\right|, \ln 2 \pi$ 가 $i$ 에 대해 독립
$$
\rightarrow g_i(x)=-\frac{\left\|x-\mu_i\right\|^2}{2 \sigma^2}+\ln P\left(\omega_i\right)
$$
여기서 $\left\|x-\mu_i\right\|^2=\left(x-\mu_i\right)^t\left(x-\mu_i\right)$ 이며, 유클리드 놈을 나타냄.
- $g_i(\boldsymbol{x})=-\frac{1}{2 \sigma^2}\left[\boldsymbol{x}^t \boldsymbol{x}-2 \boldsymbol{\mu}_i^\tau \boldsymbol{x}+\boldsymbol{\mu}_i^\tau, \boldsymbol{\mu}_i\right]+\ln P\left(\omega_i\right)$
$g_i(x)=\boldsymbol{w}_{\boldsymbol{i}}^t \boldsymbol{x}+\omega_{i 0}$ 여기서 $w_i=\frac{1}{\sigma^2} \boldsymbol{\mu}_i$ and $\omega_{i 0}=\frac{-1}{2 \sigma^2} \boldsymbol{\mu}_i^t \boldsymbol{\mu}_i+\ln P\left(\omega_i\right)$
- 선형 식 $g_i(x)=g_j(x)$ 에 의해 정의되는 초평면들
$\mathbf{w}^t\left(\mathbf{x}-\mathbf{x}_0\right)$ 여기서 $\mathbf{w}=\boldsymbol{\mu}_i-\boldsymbol{\mu}_j$ and $\mathbf{x}_0=\frac{1}{2}\left(\boldsymbol{\mu}_i+\boldsymbol{\mu}_j\right)-\frac{\sigma^2}{\left\|\boldsymbol{\mu}_i-\boldsymbol{\mu}_j\right\|^2} \ln \frac{P\left(\omega_i\right)}{P\left(\omega_j\right)}\left(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j\right)$
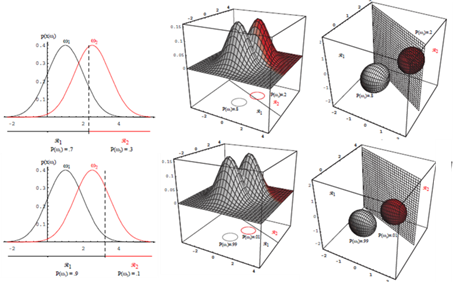
Case2: $\boldsymbol{\Sigma}_{\boldsymbol{i}}=\boldsymbol{\Sigma}$
- 모든 클래스의 공분산 행렬이 동일하다.
- 샘플들이 같은 크기와 모양의 초타원체 클러스터에 놓이는 상황에 해당
- $i$ 번째 클래스의 클러스터는 평균 벡터 $\boldsymbol{\mu}_i$ 를 중심으로 한다.
$g_i(x)=-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_{\boldsymbol{i}}\right)^t \boldsymbol{\Sigma}_i^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)-\frac{d}{2} \ln 2 \pi-\frac{1}{2} \ln \left|\boldsymbol{\Sigma}_i\right|+\ln P\left(\omega_i\right)$
$\frac{d}{2} \ln 2 \pi,\left|\boldsymbol{\Sigma}_i\right|$ 가 $i$ 에 대해 독립
$$
\rightarrow g_i(\boldsymbol{x})=-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)^t \boldsymbol{\Sigma}_i^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)-\ln P\left(\omega_i\right)
$$
- $i$ 에 독립적인 2차 항 $\boldsymbol{x}^t \boldsymbol{\Sigma}_i^{-1} \boldsymbol{x}$ 를 빼면,
$g_i(\boldsymbol{x})=\boldsymbol{w}_i \boldsymbol{x}+\omega_{i 0}$ 여기서 $\boldsymbol{w}_i=\boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}_i$ and $\omega_{i 0}=-\frac{1}{2} \boldsymbol{\mu}_i^t \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}_i+\ln P\left(\omega_i\right) $
이 판별식들은 선형적이므로 그로 인한 경계는 초평면이다. 이 초평면의 경계 식은.
$\boldsymbol{w}^t\left(\boldsymbol{x}-\boldsymbol{x}_0\right)=1$ where $\boldsymbol{w}_i=\boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}_i$ and $\boldsymbol{x}_0=\frac{1}{2}\left(\boldsymbol{\mu}_i+\boldsymbol{\mu}_j\right)-\frac{\ln \left[P\left(\omega_i\right) / P\left(\omega_j\right)\right]}{\left(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j\right)^t \boldsymbol{\Sigma}^{-1}\left(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j\right)}\left(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j\right)$
- $\boldsymbol{w}=\boldsymbol{\Sigma}^{-1}\left(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j\right)$ 는 일반적으로 $\boldsymbol{\mu}_i-\boldsymbol{\mu}_j$ 방향이 아니기 때문에 영역을 분리하는 초평면은 일반적으로 이 평균들을 잇는 선에 직교하지 않는다.
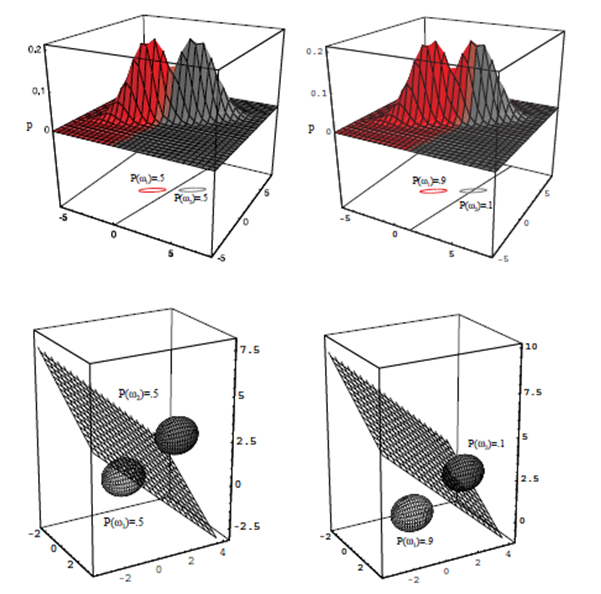
Case3: $\Sigma_i=\operatorname{arbitrary}($ (임의적)
- 일반적인 정규분포의 경우 공분산 행렬은 각 부류마다 다르다.
$$
\begin{aligned}
& g_i(x)=-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)^t \boldsymbol{\Sigma}_i^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)-\frac{d}{2} \ln 2 \pi-\frac{1}{2} \ln \left|\boldsymbol{\Sigma}_i\right|+\ln P\left(\omega_i\right) \\
& \frac{1}{2} \ln 2 \pi \text { 만이 i에 대해 독립 } \\
& \rightarrow g_i(\boldsymbol{x})=\boldsymbol{x}^t \boldsymbol{W}_i \boldsymbol{x}+\boldsymbol{w}_i^t \boldsymbol{x}+\omega_{i 0^2} \\
& \text { where, } \boldsymbol{W}_i=-\frac{1}{2} \boldsymbol{\Sigma}_i^{-1}, \boldsymbol{w}_i=\boldsymbol{\Sigma}_i^{-1} \boldsymbol{\mu}_i \text { and } \\
& \omega_{i 0}=-\frac{1}{2} \boldsymbol{\mu}_i^t \boldsymbol{\Sigma}_i^{-1} \boldsymbol{\mu}_i-\frac{1}{2} \ln \left|\boldsymbol{\Sigma}_i\right|+\ln P\left(\omega_i\right)
\end{aligned}
$$
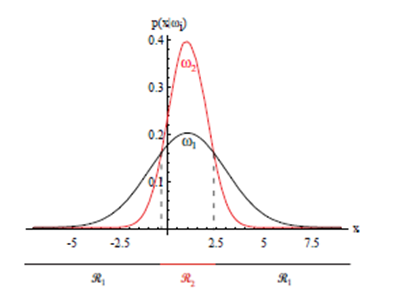

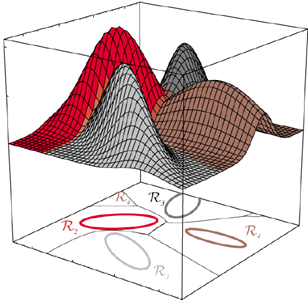
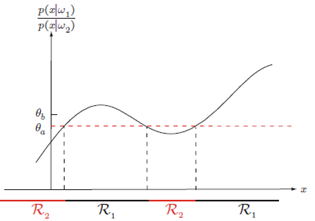
EXAMPLE1: 2차원 가우스 데이터에 대한 판정 영역
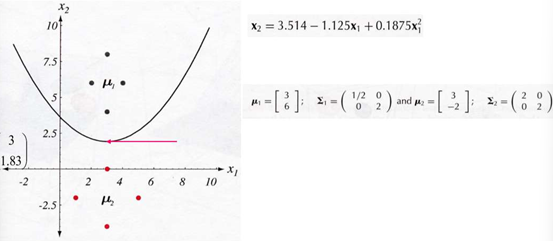
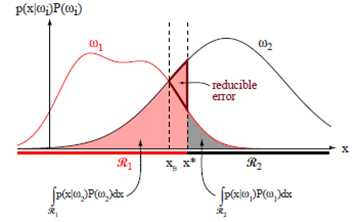
정규 분포의 오차 범위
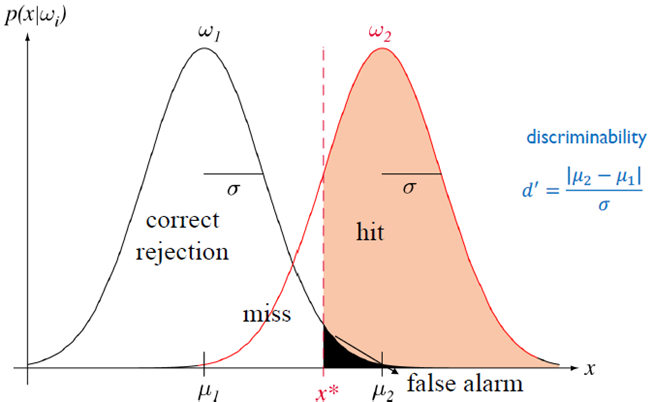
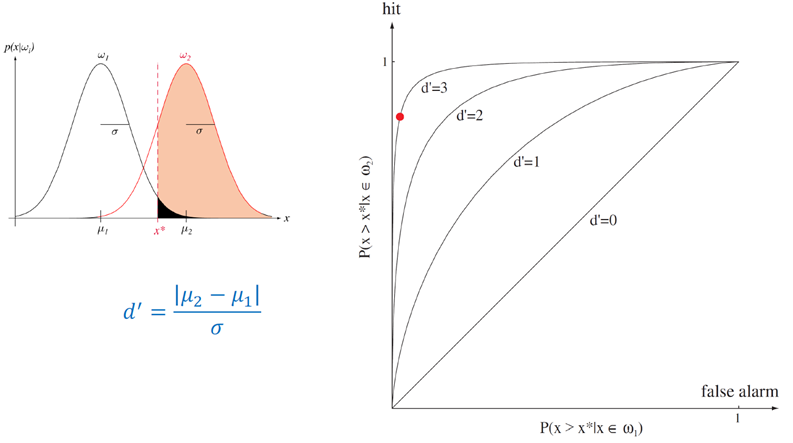
ROC(receiver operation characteristic)(수신기 동작 특성)
Bayes decision theory-이산적 특징
- 많은 실제 응용에서 구성요소 (특징벡터) x 는 2진, 3진, 또는 더 높은 진수의 정수값을 가지고, $x$ 는 $m$ 개의 이산 값 $v_1, \ldots, v_m$ 중 하나만 취할 수 있다.
$$
\int p\left(x \mid \omega_j\right) d x \rightarrow \sum_x P\left(x \mid \omega_j\right)
$$
- bayes 공식은 확률 밀도가 아닌 확률들을 포함
$$
P\left(\omega_j \mid x\right)=\frac{P\left(x \mid \omega_j\right) P\left(\omega_j\right)}{P(x)} \quad P(x)=\sum_{j=1}^c P\left(x \mid \omega_j\right) P\left(\omega_j\right)
$$
- 조건부 리스크 $R(\alpha \mid x)$ 의 정의는 변하지 않으며, bayes판정 룰도 동일하다.
- 사후 확률을 최대화하여 오류율을 최소화하는 기본 룰도 바뀌지 않는다.
독립적 2진 특징
- 특징 벡터의 요소들이 2진 값이고, 조건부 독립인 2부류 문제를 고려
$$
\begin{aligned}
& \text { Let } x=\left(x_1, \ldots, x_d\right)^t \text { 여기서 요소 } x_i \text { 는 } 0 \text { 또는 } 1 \text { 로 놓고 확률들은 다음과 같다. } \\
& p_i=\operatorname{Pr}\left[x_i=1 \mid \omega_1\right] \text { and } q_i=\operatorname{Pr}\left[x_i=1 \mid \omega_2\right] \\
& \rightarrow P\left(x \mid \omega_1\right)=\prod_{i=1}^d p_i^{x_i}\left(1-p_i\right)^{1-x_i} \text { and } P\left(x \mid \omega_2\right)=\prod_{i=1}^d q_i^{x_i}\left(1-q_i\right)^{1-x_i} \\
&
\end{aligned}
$$
그럼 우도비는
$$
\frac{P\left(x \mid \omega_1\right)}{P\left(x \mid \omega_2\right)}=\prod_{i=1}^d\left(\frac{p_i}{q_i}\right)^{x_i}\left(\frac{1-p_i}{1-q_i}\right)^{1-x_i}
$$
$$
\begin{aligned}
& \text { - 판별함수 }\left(g(x)=P\left(\omega_1 \mid x\right)-P\left(\omega_2 \mid x\right)-(30), g(x)=\ln \frac{p\left(x \mid \omega_1\right)}{p\left(x \mid \omega_2\right)}+\ln \frac{P\left(\omega_1\right)}{P\left(\omega_2\right)}-(31)\right. \text { 로 부터) } \\
& g(x)=\sum_{i=1}^d\left[x_i \ln \frac{p_i}{q_i}+\left(1-x_i\right) \ln \frac{1-p_i}{1-q_i}\right]+\ln \frac{P\left(\omega_1\right)}{P\left(\omega_2\right)}
\end{aligned}
$$
- 이 판별 함수는 $x_i$ 에서 선형적이다. 따라서...
$$
\begin{aligned}
g(\boldsymbol{x}) & =\sum_{i=1}^d \omega_i x_i+\omega_0 \\
\text { 여기서 } \omega_i=\ln \frac{p_i\left(1-q_i\right)}{q_i\left(1-p_i\right)} \quad i=1, \ldots, d \quad & \omega_0=\sum_{i=1}^d \ln \frac{1-p_i}{1-q_i}+\ln \left(\frac{P\left(\omega_1\right)}{P\left(\omega_2\right)}\right)
\end{aligned}
$$
'IT > 수업내용 정리' 카테고리의 다른 글
| AIE_6208_pattern recognition_ch01 Intro (0) | 2022.12.21 |
|---|---|
| CSE_5311_Chapter 2: 입/출력 end 복잡도 분석 (0) | 2022.11.18 |
| CSE_5311_Chapter 01: 음성인식 연구 동향 및 문제 정의 (1) | 2022.11.18 |



