
Primary Reference:
Social Media Mining Reza Zafarani, Mohammad-Ali Abbasi, Huan Liu, Cambridge University Press 2014,http://socialmediamining.info
Social Media Mining
Social Media Mining An Introduction A Textbook by Cambridge University Press Syracuse University LinkedIn Arizona State University Accessed 150,000+ times from 180+ countries and 2000+ Universities The growth of social media over the last decade has revolu
www.socialmediamining.info
OVER VIEW


소셜 미디어는 인터넷 플랫폼을 이용해, 정보 및 경험을 보다 효율적으로 다른 사람들과 공유하고 토론하는 것을 명칭한다.
소셜 미디어의 주요 특성은 다음과 같다:
1. Participation- 소셜 미디어는 많은 사람의 기여와 피드백을 장려함으로, 미디어와 관객의 경계를 모호하게 만든다.
2. Openness- 대부분의 소셜 미디어 서비스는 피드백과 참여에 열려있으며, 투표, 의견 및 정보공유를 장려한다.
3. Conversation- 전통적 미디어는 일방적 소통이지만 소셜 미디어는 양방향 소통이다
4. Community - 소셜 미디어는 같은 관심사를 공유한 사람들간 커뮤니티가 빠르게 형성되고 소통이 가능하다
5. Connectedness - 대부분의 소셜 미디어는 링크를 사용한 연결성을 기반한다.
소셜 미디어 마이닝의 Challenges:
1. Big Data Paradox
- 소셜 미디어 데이터는 매우 방대하지만, 편향적인 특성이 있다. (어떤 사람은 친구가 1000명이고 어떤 사람은 10명.. )
- 개인의 입장에서는 연결된(가용할 수 있는) data가 적다.
2. Obtaining Sufficient Samples
- 충분한 샘플을 얻기가 힘들다. (특정 샘을이 전체 데이터를 대표한다고 볼 수 있는가..)
3. Noise Removal Fallacy
- 노이즈를 너무 많이 제거하면 데이터가 sparse해진다.
- 노이즈의 정의가 상대적이고 복잡하며 작업에 따라 다르다(어떤 주제에서의 노이즈도 다른 주제에서는 노이즈가 아닐수 있음)
4. Evaluation Dilemms
- 정답이 없기때문에, 평가가 어렵다. 근거가 없으면 어떻게 평가를 할수 있는가?
#2_SMM_Graph Essentials

Bridges of konigsberg 문제는, 두개의 섬과 강의로 나뉜 대륙이 7개의 다리로 연결 되어 있을때, 다리를 한번씩만 건너서 모든 곳을 방문할 수 있는가의 문제이다.
이 문제를 해결하는 방법은 그래프 표현을 이용하는 것으로, 오일러는 걷기의 시작, 끝을 제외하고 다른 모든 노드에 들어가고 나와야 하므로 이러한 노드에는 짝수개의 다리가 연결되어야 함을 증명했다.
네트워크는 그래프로 표현할 수 있고, (node -> route, connection->연결망) 네트워크 문제는 일반적으로 그래프 이론으로 나타낼 수 있다.

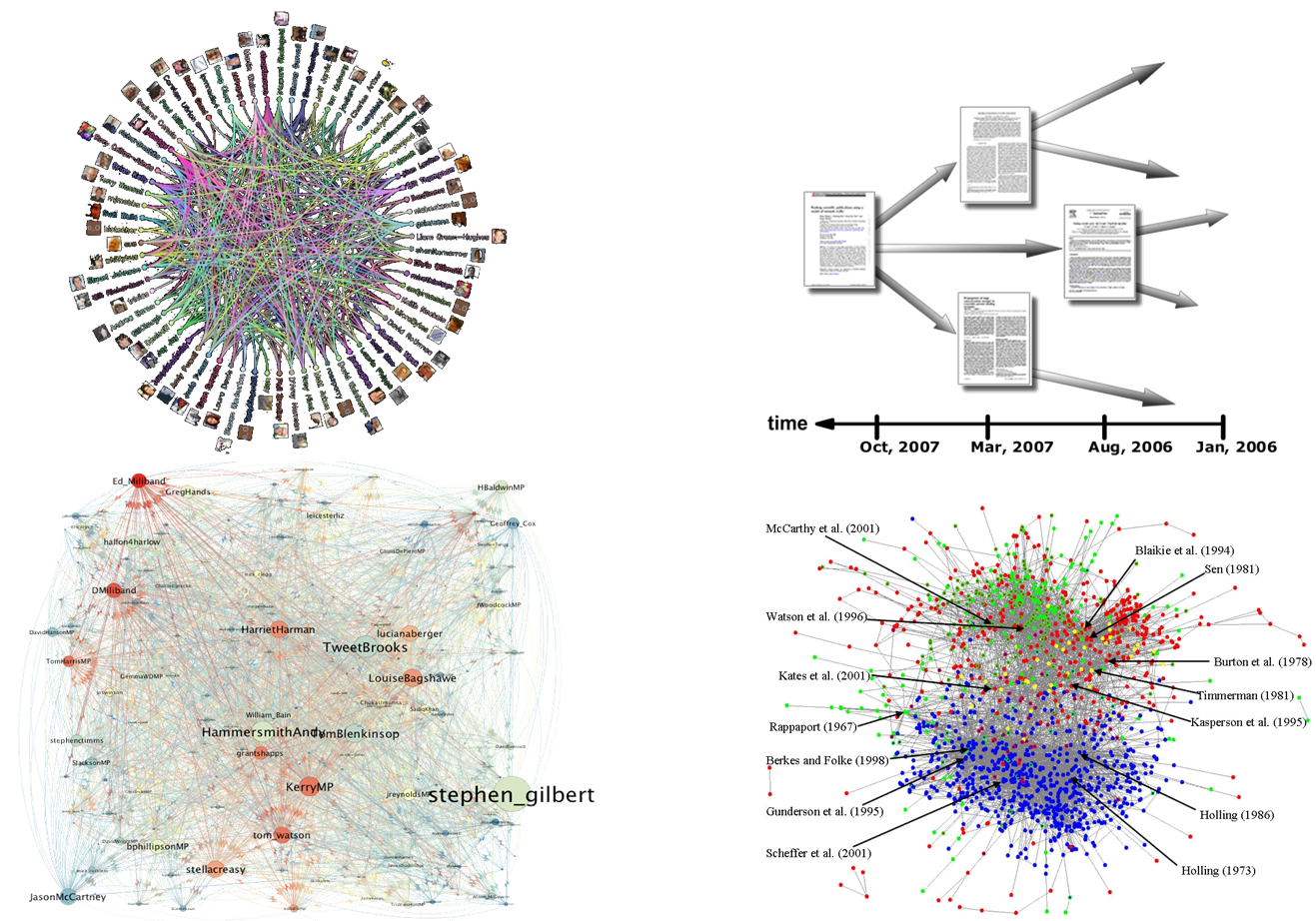

인터넷의 시각화
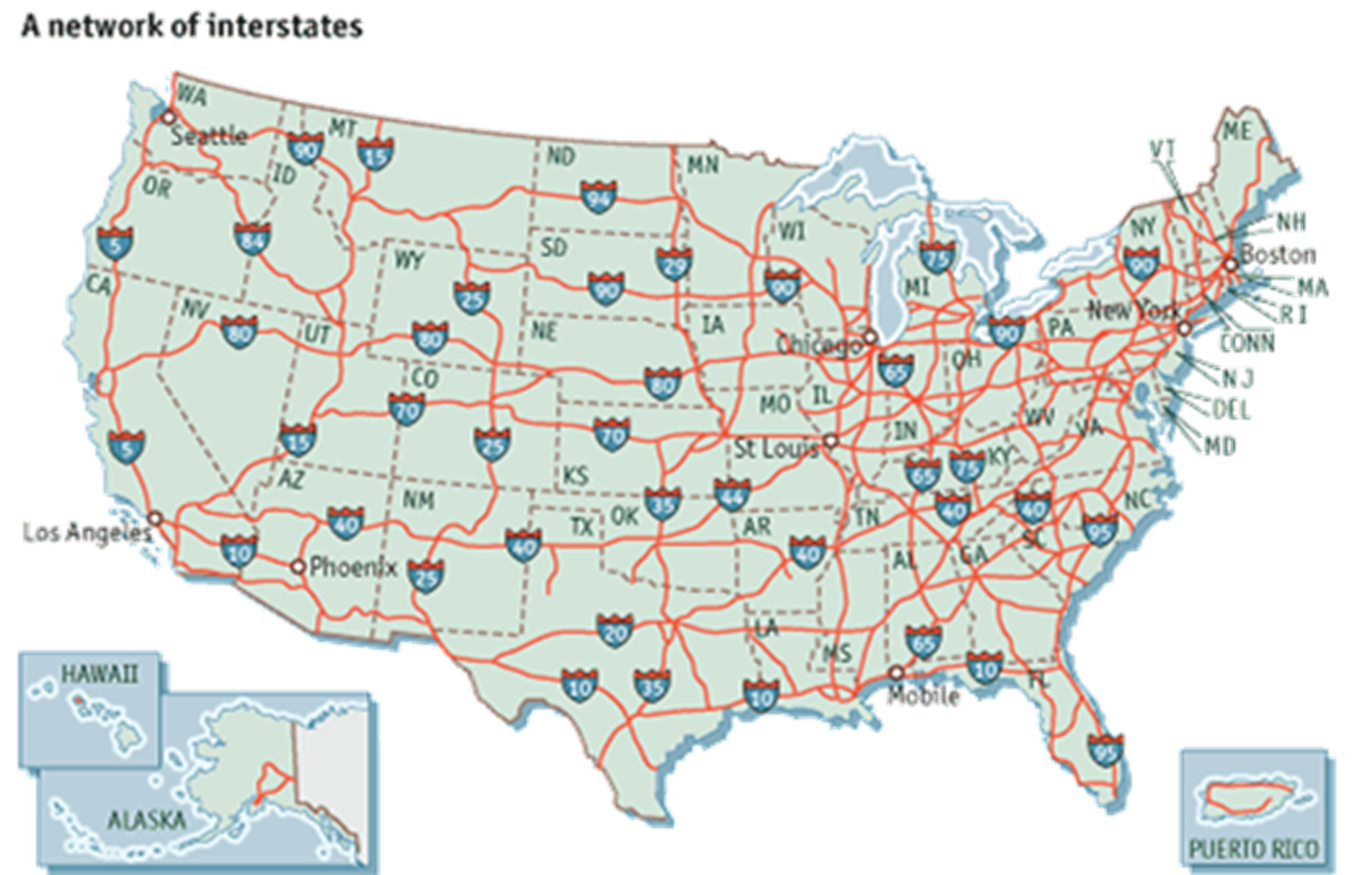
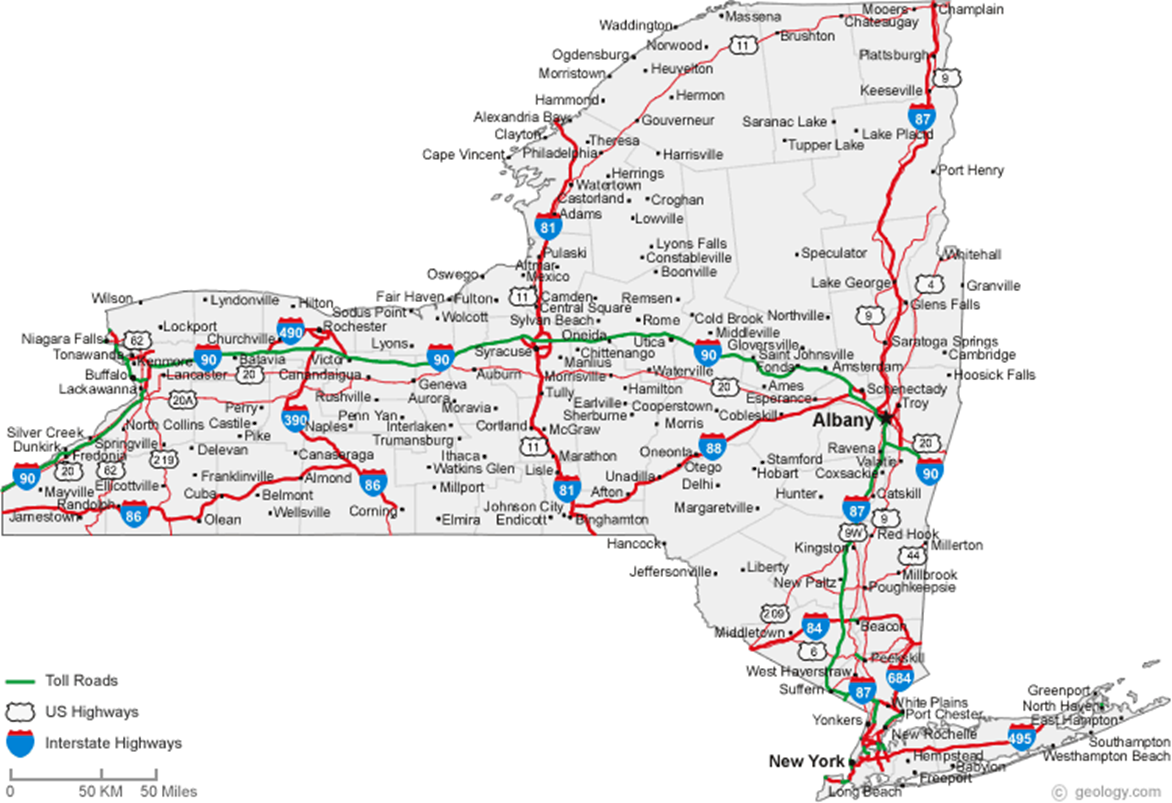
소셜 네트워크 분석은 사회과학, 통계, 그래프 이론, 복잡한 네트워크, 컴퓨터 과학의 연합 분야라고 할 수 있다.
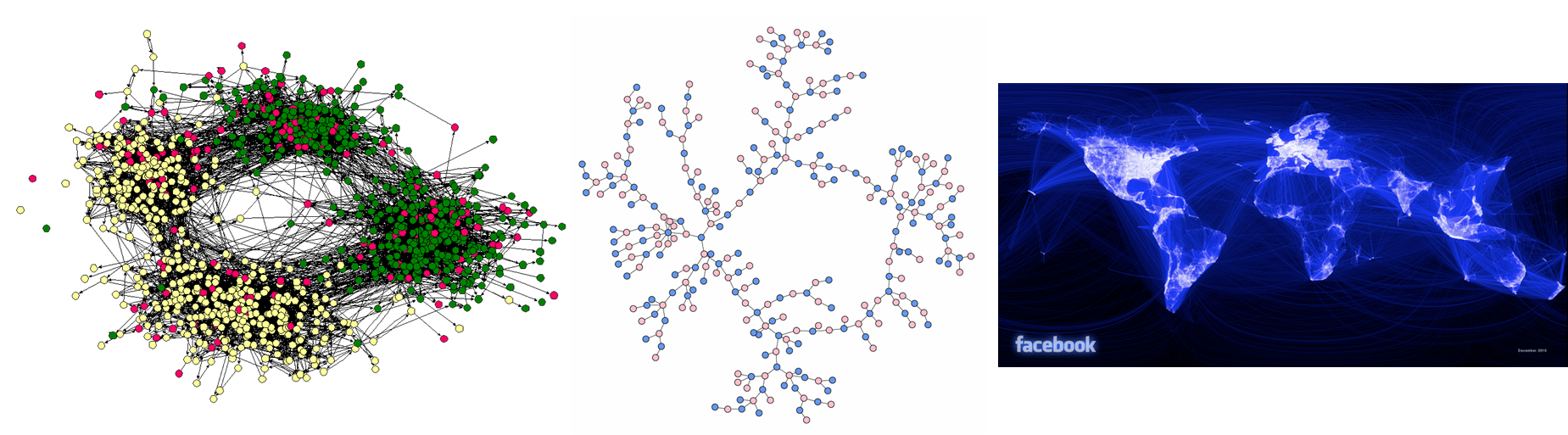
- 그래프의 기초
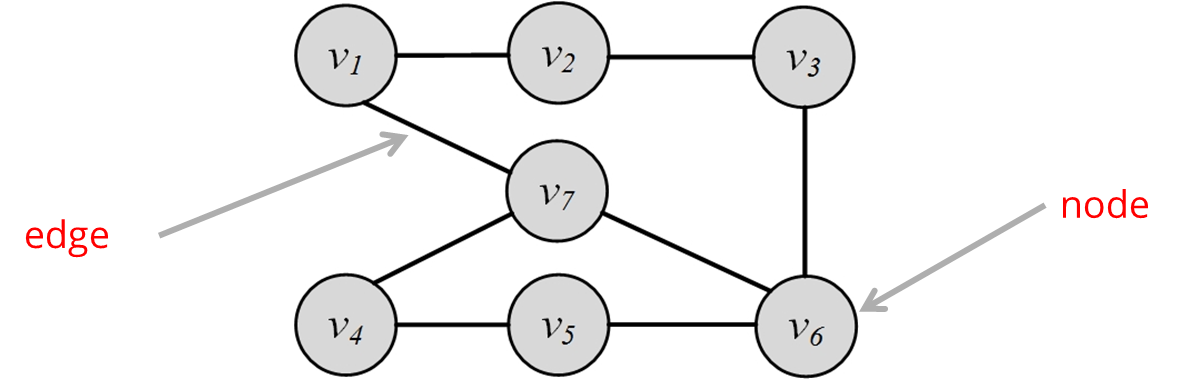
네트워크는 그래프 또는 선으로 연결된 점의 집합이라 할 수 있다.
점은 node, actor, vertices, vertex 등으로 볼수 있고
연결은 edges, ties라고 볼 수 있다.
그래프의 노드 V는 V={v_1, v_2, ..., v_n}로 나타내고, size of the graph |V|=n
Edge는 node간의 ties, relationships를 나타내며 다음과 같이 표현한다.
E = {e_1, e_2, ..., e_m}
Number is edgs( size of the edge-set):|E|=m
edge는 e(v1,v2)와 같이 표현하며, 방향성이 있는 경우와 없는 경우가 있다.
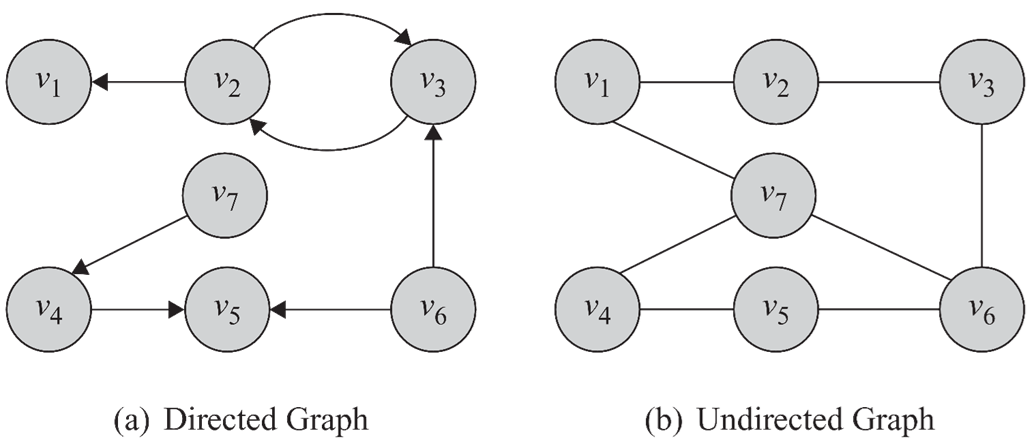
(a)의 경우 e(v2,v1)과 e(v1,v2)는 다르지만, 방향성이 없는 (b)에서는 동일한 표현이다.
어떤 노드 V가 있을 때 연결된 노드를 neighborhood라 하고, N(v)라고 표현한다.
(b)에서 N(v7)={v1, v4, v6}
방향성이 있는 그레프의 경우 in, out가 존재하므로 Nin(v), Nout(v)로 표현한다.
Degree(차수)와 차수 분포
- 방향성이 없는 그래프에서 degree의 합은 edge수의 2배이다.
\sum(d_i)=2|E|
- degree의 합은 짝수이다.
- 모든 방향성있는 그래프에서 in-degrees의 합은 out-degrees의 합과 같다.
'IT' 카테고리의 다른 글
| machine learning Basic #01_Supervised Learning_Classification(작성중) (0) | 2022.09.22 |
|---|---|
| 낡은 nas j4105로 교체기. (4) | 2018.02.26 |



